комит
4addc5dc28
48 измењених фајлова са 111788 додато и 0 уклоњено
+ 307
- 0
README.md
Прегледај датотеку
| # A Sage Toolkit to attack and estimate the hardness of LWE with Side Information | |||||
| This repository contains the artifacts associated to the article | |||||
| [DDGR20] **LWE with Side Information: Attacks and Concrete Security Estimation** | |||||
| by _Dana Dachman-Soled, Léo Ducas, Huijing Gong, Mélissa Rossi_ | |||||
| https://eprint.iacr.org/2020/292.pdf | |||||
| The code is written for Sage 9.0 (Python 3 Syntax). | |||||
| ## Organization | |||||
| The library itself is to be found in the `framework` folder. | |||||
| `Sec5.2_validation` and `Sec6_applications` contain the code to reproduce our experiments. | |||||
| ## How to use the full-fledged version | |||||
| The full-fledged implementation is called when the class of the instance is DBDD. Let us create a small LWE instance and estimate its security in bikz. The code should be run from the directories `Sec5.2_validation` or `Sec6_applications`. | |||||
| ```sage | |||||
| sage: load("../framework/instance_gen.sage") | |||||
| ....: n = 70 | |||||
| ....: m = n | |||||
| ....: q = 3301 | |||||
| ....: D_s = build_centered_binomial_law(40) | |||||
| ....: D_e = D_s | |||||
| ....: A, b, dbdd = initialize_from_LWE_instance(DBDD, n, q, m, D_e, D_s) | |||||
| ....: # In such parameter range, no need to integrate q-vectors | |||||
| ....: beta, delta = dbdd.estimate_attack() | |||||
| ``` | |||||
| ```text | |||||
| Build DBDD from LWE | |||||
| n= 70 m= 70 q=3301 | |||||
| Attack Estimation | |||||
| dim=141 δ=1.012362 β=45.40 | |||||
| ``` | |||||
| Our full-fledged implementation contains an attack procedure that runs BKZ with iterating gradually the block size. It then compares the recovered secret with the actual one. | |||||
| ```sage | |||||
| sage: secret = dbdd.attack() | |||||
| ``` | |||||
| ```text | |||||
| Running the Attack | |||||
| Running BKZ-42 Success ! | |||||
| ``` | |||||
| Here, the block size stopped at 42 while an average blocksize of 45.40 has been estimated. Let us now create four vectors v for making perfect hints. To simulate side information, we compute the hints with the function dbdd.leak(v). | |||||
| ```sage | |||||
| sage: # Simulating perfect hints | |||||
| ....: v0 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: v1 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: v2 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: v3 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: # Computing l = <vi, s> | |||||
| ....: dbdd.leak(v0), dbdd.leak(v1), dbdd.leak(v2), dbdd.leak(v3) | |||||
| ``` | |||||
| ```text | |||||
| (27, -62, -45, -47) | |||||
| ``` | |||||
| Let us now integrate the perfect hints into our instance. | |||||
| ```sage | |||||
| sage: # Integrate perfect hints | |||||
| ....: _ = dbdd.integrate_perfect_hint(v0, 27) | |||||
| ....: _ = dbdd.integrate_perfect_hint(v1, -62) | |||||
| ....: _ = dbdd.integrate_perfect_hint(v2, -45) | |||||
| ....: _ = dbdd.integrate_perfect_hint(v3, -47) | |||||
| ``` | |||||
| ```text | |||||
| integrate perfect hint u0 + u1 + u7 + u8 + u9 + ... = 27 Worthy hint ! dim=140, δ=1.01252643, β=41.93 | |||||
| integrate perfect hint u0 + u2 + u8 + u9 + u10 + ... = -62 Worthy hint ! dim=139, δ=1.01275412, β=38.42 | |||||
| integrate perfect hint u0 + u1 + u3 + u4 + u7 + ... = -45 Worthy hint ! dim=138, δ=1.01293851, β=34.78 | |||||
| integrate perfect hint u1 + u9 + u11 + u12 + u13 + ... = -47 Worthy hint ! dim=137, δ=1.01314954, β=30.91 | |||||
| ``` | |||||
| The cost of the lattice attack has decreased by around 14 bikz. Let us now create four vectors v for making modular hints. To simulate side information, we compute the hint with the function dbdd.leak(v) with different moduli. | |||||
| ```sage | |||||
| sage: # Simulating modular hints | |||||
| ....: v0 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: v1 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: v2 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: v3 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: # Computing l = <vi, s> mod k | |||||
| ....: dbdd.leak(v0)%2, dbdd.leak(v1)%3, dbdd.leak(v2)%4, dbdd.leak(v3)%5 | |||||
| ``` | |||||
| ```text | |||||
| (1, 1, 2, 3) | |||||
| ``` | |||||
| Let us now integrate the modular hints into our instance. We assume smoothness. In other words, the lattice is sparsified but the covariance matrix and average remain the same. | |||||
| ```sage | |||||
| sage: # Integrate modular hints | |||||
| ....: _ = dbdd.integrate_modular_hint(v0, 1, 2, True) | |||||
| ....: _ = dbdd.integrate_modular_hint(v1, 1, 3, True) | |||||
| ....: _ = dbdd.integrate_modular_hint(v2, 2, 4, True) | |||||
| ....: _ = dbdd.integrate_modular_hint(v3, 3, 5, True) | |||||
| ``` | |||||
| ```text | |||||
| integrate modular hint (smooth) u2 + u3 + u4 + ... = 1 MOD 2 Worthy hint ! dim=137, δ=1.01318729, β=30.55 | |||||
| integrate modular hint (smooth) u0 + u2 + u10 + ... = 1 MOD 3 Worthy hint ! dim=137, δ=1.01319931, β=29.98 | |||||
| integrate modular hint (smooth) u0 + u4 + u9 + ... = 2 MOD 4 Worthy hint ! dim=137, δ=1.01327415, β=29.24 | |||||
| integrate modular hint (smooth) u2 + u3 + u6 + ... = 3 MOD 5 Worthy hint ! dim=137, δ=1.01331577, β=28.37 | |||||
| ``` | |||||
| As modular hints contain less information than perfect ones, especially for low modulus, the cost of the lattice attack decreased by only 3 bikz. Let us do the same for approximate hints. To simulate side information, we compute the hint with the function dbdd.leak(v) and manually change the value to represent the measurement noise. | |||||
| ```sage | |||||
| sage: # Simulating approximate hints | |||||
| ....: v0 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: v1 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: v2 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: v3 = vec([randint(0, 1) for i in range(m + n)]) | |||||
| ....: # Computing l = <vi, s> + noise | |||||
| ....: dbdd.leak(v0) + 2, dbdd.leak(v1) + 1, dbdd.leak(v2) - 1, dbdd.leak(v3) | |||||
| ``` | |||||
| ```text | |||||
| (-19, -29, -16, 1) | |||||
| ``` | |||||
| Let us now integrate the approximate hints into our instance. We assume that we want to condition the new information with the prior one and not to erase the previous distribution. | |||||
| ```sage | |||||
| sage: # Integrate approximate hints | |||||
| ....: var = 10 | |||||
| ....: _ = dbdd.integrate_approx_hint(v0, -19, var, aposteriori=False) | |||||
| ....: _ = dbdd.integrate_approx_hint(v1, -29, var, aposteriori=False) | |||||
| ....: _ = dbdd.integrate_approx_hint(v2, -16, var, aposteriori=False) | |||||
| ....: _ = dbdd.integrate_approx_hint(v3, 1, var, aposteriori=False) | |||||
| ``` | |||||
| ```text | |||||
| integrate approx hint (conditionning) | |||||
| u0 + u4 + u5 + u6 + u8 + ... = -19 + χ(σ²=10.000) Worthy hint ! dim=137, δ=1.01322376, β=29.74 | |||||
| integrate approx hint (conditionning) | |||||
| u0 + u5 + u6 + u7 + u8 + ... = -29 + χ(σ²=10.000) Worthy hint ! dim=137, δ=1.01329667, β=28.56 | |||||
| integrate approx hint (conditionning) | |||||
| u0 + u4 + u5 + u7 + u12 + ... = -16 + χ(σ²=10.000) Worthy hint ! dim=137, δ=1.01337366, β=27.24 | |||||
| integrate approx hint (conditionning) | |||||
| u1 + u2 + u3 + u4 + u5 + ... = 1 + χ(σ²=10.000) Worthy hint ! dim=137, δ=1.01340026, β=25.77 | |||||
| ``` | |||||
| Here, the cost of the lattice reduction attack has decreased by 3 bikz. | |||||
| While all the hints have been integrated, we finally estimate the security and run the attack again. | |||||
| ```sage | |||||
| sage: beta, delta = dbdd.estimate_attack() | |||||
| ....: secret = dbdd.attack() | |||||
| ``` | |||||
| ```text | |||||
| Attack Estimation | |||||
| dim=137 δ=1.013400 β=25.77 | |||||
| Running the Attack | |||||
| Running BKZ-27 Success ! | |||||
| ``` | |||||
| This time, BKZ stopped at blocksize 27 while the estimation was around 26 bikz. | |||||
| ## How to use the lightweight version | |||||
| The lightweight implementation is called when the class of the DBDD instance is `DBDD_predict`. While the heavy basis of the lattice is not stored, only its volume and dimension are stored. Let us create an LWE instance. Before estimating the cost of the lattice reduction attack in bikz, one needs to integrate the q vectors (i.e. drop some LWE samples). Then, the security is computed in bikz thanks to the volume and dimension of the lattice. | |||||
| ```sage | |||||
| sage: load("../framework/instance_gen.sage") | |||||
| ....: n = 512 | |||||
| ....: m = n | |||||
| ....: q = 2 ^ 15 | |||||
| ....: D_e = {-2: 0.05, -1: 0.20, 0: 0.5, 1: 0.20, 2: 0.05} | |||||
| ....: D_s = D_e | |||||
| ....: A, b, dbdd = initialize_from_LWE_instance(DBDD_predict, n, q, m, D_e, D_s) | |||||
| ....: _ = dbdd.integrate_q_vectors(q, report_every=20) | |||||
| ....: beta, delta = dbdd.estimate_attack() | |||||
| ``` | |||||
| ```text | |||||
| Build DBDD from LWE | |||||
| n=512 m=512 q=32768 | |||||
| Integrating q-vectors | |||||
| [...20] integrate short vector hint | |||||
| Worthy hint ! dim=1024, δ=1.00518248, β=270.72 | |||||
| Attack Estimation | |||||
| dim=1016 δ=1.005183 β=270.69 | |||||
| ``` | |||||
| We now create a new LWE instance (necessary because the q vectors should always been included at the end). And, we create 4 vectors and simulate side information. Here we only integrate perfect hints. | |||||
| ```sage | |||||
| sage: load("../framework/instance_gen.sage") | |||||
| ....: A, b, dbdd = initialize_from_LWE_instance(DBDD_predict, n, q, m, D_e, D_s) | |||||
| ....: # Simulating hints | |||||
| ....: v0 = vec([1 if i < m / 2 else 0 for i in range(m + n)]) | |||||
| ....: v1 = vec([0 if i < m / 2 else 1 for i in range(m + n)]) | |||||
| ....: v2 = vec([1 if i < m else 0 for i in range(m + n)]) | |||||
| ....: v3 = vec([1 if i < m / 4 else 0 for i in range(m + n)]) | |||||
| ....: # Computing l = <vi, s> | |||||
| ....: dbdd.leak(v0), dbdd.leak(v1), dbdd.leak(v2), dbdd.leak(v3) | |||||
| ``` | |||||
| ```text | |||||
| Build DBDD from LWE | |||||
| n=512 m=512 q=32768 | |||||
| (33, 9, 56, 12) | |||||
| ``` | |||||
| The hints must be now integrated and we assess the lattice reduction cost. Due to the shape of our vectors, new short vector hints must be integrated. | |||||
| ```sage | |||||
| sage: # Integrate hints | |||||
| ....: _ = dbdd.integrate_perfect_hint(v0, 33) | |||||
| ....: _ = dbdd.integrate_perfect_hint(v1, 9) | |||||
| ....: _ = dbdd.integrate_perfect_hint(v2, 56) | |||||
| ....: _ = dbdd.integrate_perfect_hint(v3, 12) | |||||
| ....: M = q * identity_matrix(n + m) | |||||
| ....: V = vec(M[0] - M[1]) | |||||
| ....: i = 0 | |||||
| ....: while dbdd.integrate_short_vector_hint(V): | |||||
| ....: i += 1 | |||||
| ....: V = vec(M[i] - M[i + 1]) | |||||
| ....: beta, delta = dbdd.estimate_attack() | |||||
| ``` | |||||
| ```text | |||||
| integrate perfect hint u0 + u1 + u2 + u3 + u4 + ... = 33 Worthy hint ! dim=1024, δ=1.00519338, β=269.83 | |||||
| integrate perfect hint u256 + u257 + u258 + u259 ... = 9 Worthy hint ! dim=1023, δ=1.00520492, β=268.91 | |||||
| integrate perfect hint u0 + u1 + u2 + u3 + u4 + ... = 56 Worthy hint ! dim=1022, δ=1.00521752, β=268.03 | |||||
| integrate perfect hint u0 + u1 + u2 + u3 + u4 + ... = 12 Worthy hint ! dim=1021, δ=1.00522793, β=267.19 | |||||
| integrate short vector hint 32768*c0 - 32768*c1 ∈ Λ Not sure if in Λ, Unworthy hint, Rejected. | |||||
| Attack Estimation | |||||
| dim=1021 δ=1.005228 β=267.19 | |||||
| ``` | |||||
| Here, with 4 perfect hints, the cost of the lattice reduction attack has decreased by around 3 bikz. The blocksize may be actually below 267.19 as there may be residual short vector hints. | |||||
| ## How to use the super lightweight version | |||||
| The super lightweight implementation is called when the class of the instance is `DBDD_predict_diag`. Here, we assume that the covariance matrix is always diagonal. Let us create an LWE instance. We integrate the q vectors (i.e. drop some LWE samples) and compute the security in bikz. | |||||
| ```sage | |||||
| sage: load("../framework/instance_gen.sage") | |||||
| ....: n = 512 | |||||
| ....: m = n | |||||
| ....: q = 2 ^ 15 | |||||
| ....: D_e = {-2: 0.05, -1: 0.20, 0: 0.5, 1: 0.20, 2: 0.05} | |||||
| ....: D_s = D_e | |||||
| ....: A, b, dbdd = initialize_from_LWE_instance(DBDD_predict_diag, n, q, m, D_e, D_s) | |||||
| ....: _ = dbdd.integrate_q_vectors(q, report_every=20) | |||||
| ....: beta, delta = dbdd.estimate_attack() | |||||
| ``` | |||||
| ```text | |||||
| Build DBDD from LWE | |||||
| n=512 m=512 q=32768 | |||||
| Integrating q-vectors | |||||
| [...20] integrate short vector hint Worthy hint ! dim=1024, δ=1.00518248, β=270.72 | |||||
| Attack Estimation | |||||
| dim=1016 δ=1.005183 β=270.69 | |||||
| ``` | |||||
| We create 20 canonical (necessary to keep the covariance matrix diagonal) vectors for integrating perfect hints. | |||||
| ```sage | |||||
| sage: A, b, dbdd = initialize_from_LWE_instance(DBDD_predict_diag, n, q, m, D_e, D_s) | |||||
| ....: # Simulating hints | |||||
| ....: v = [[] for _ in range(20)] | |||||
| ....: for i in range(20): | |||||
| ....: v[i] = canonical_vec(m + n, i) | |||||
| ``` | |||||
| ```text | |||||
| Build DBDD from LWE | |||||
| n=512 m=512 q=32768 | |||||
| ``` | |||||
| The perfect hints are integrated into a new instance and the security is estimated. | |||||
| ```sage | |||||
| sage: # Integrate hints | |||||
| ....: for i in range(20): | |||||
| ....: _ = dbdd.integrate_perfect_hint(v[i], dbdd.leak(v[i])) | |||||
| ....: _ = dbdd.integrate_q_vectors(q, report_every=20) | |||||
| ....: beta, delta = dbdd.estimate_attack() | |||||
| ``` | |||||
| ```text | |||||
| integrate perfect hint u0 = -2 Worthy hint ! dim=1024, δ=1.00519245, β=270.02 | |||||
| integrate perfect hint u1 = -1 Worthy hint ! dim=1023, δ=1.00520080, β=269.31 | |||||
| integrate perfect hint u2 = 1 Worthy hint ! dim=1022, δ=1.00520918, β=268.61 | |||||
| integrate perfect hint u3 = 0 Worthy hint ! dim=1021, δ=1.00521757, β=267.91 | |||||
| integrate perfect hint u4 = 1 Worthy hint ! dim=1020, δ=1.00522774, β=267.21 | |||||
| integrate perfect hint u5 = 1 Worthy hint ! dim=1019, δ=1.00523618, β=266.51 | |||||
| integrate perfect hint u6 = 0 Worthy hint ! dim=1018, δ=1.00524465, β=265.81 | |||||
| integrate perfect hint u7 = -2 Worthy hint ! dim=1017, δ=1.00525490, β=265.11 | |||||
| integrate perfect hint u8 = 0 Worthy hint ! dim=1016, δ=1.00526341, β=264.41 | |||||
| integrate perfect hint u9 = 0 Worthy hint ! dim=1015, δ=1.00527195, β=263.71 | |||||
| integrate perfect hint u10 = 2 Worthy hint ! dim=1014, δ=1.00528229, β=263.01 | |||||
| integrate perfect hint u11 = 0 Worthy hint ! dim=1013, δ=1.00529087, β=262.32 | |||||
| integrate perfect hint u12 = 0 Worthy hint ! dim=1012, δ=1.00529947, β=261.62 | |||||
| integrate perfect hint u13 = 2 Worthy hint ! dim=1011, δ=1.00530810, β=260.93 | |||||
| integrate perfect hint u14 = 0 Worthy hint ! dim=1010, δ=1.00531856, β=260.23 | |||||
| integrate perfect hint u15 = 2 Worthy hint ! dim=1009, δ=1.00532723, β=259.54 | |||||
| integrate perfect hint u16 = 1 Worthy hint ! dim=1008, δ=1.00533593, β=258.85 | |||||
| integrate perfect hint u17 = 0 Worthy hint ! dim=1007, δ=1.00534647, β=258.16 | |||||
| integrate perfect hint u18 = -1 Worthy hint ! dim=1006, δ=1.00535522, β=257.46 | |||||
| integrate perfect hint u19 = 1 Worthy hint ! dim=1005, δ=1.00536399, β=256.77 | |||||
| Integrating q-vectors | |||||
| [...20] integrate short vector hint 32768*c1023 ∈ Λ Worthy hint ! dim=1004, δ=1.00536426, β=256.76 | |||||
| [...20] integrate short vector hint 32768*c1003 ∈ Λ Worthy hint ! dim=984, δ=1.00536755, β=256.54 | |||||
| Attack Estimation | |||||
| dim=979 δ=1.005368 β=256.53 | |||||
| ``` | |||||
| The integration of 20 perfect hints implies here a loss of 13 bikz. |
+ 3199
- 0
Sec5.2_validation/.ipynb_checkpoints/Framework Improvements-checkpoint.ipynb
Разлика између датотеке није приказан због своје велике величине
Прегледај датотеку
+ 3121
- 0
Sec5.2_validation/Framework Improvements.ipynb
Разлика између датотеке није приказан због своје велике величине
Прегледај датотеку
BIN
Sec5.2_validation/__pycache__/map_drop.cpython-37.pyc
Прегледај датотеку
+ 205
- 0
Sec5.2_validation/check_consistency.sage
Прегледај датотеку
| #!/usr/bin/sage -python | |||||
| # -*- coding: latin-1 -*- | |||||
| load("../framework/instance_gen.sage") | |||||
| def check_all_equal(du, du_): | |||||
| assert du.dim() == du_.dim() | |||||
| assert abs(du.dvol - du_.dvol) < 1e-6 | |||||
| assert abs(du.beta - du_.beta) < 1e-6 | |||||
| if du.delta == oo: | |||||
| assert du_.delta == oo | |||||
| else: | |||||
| assert abs(du.delta - du_.delta) < 1e-6 | |||||
| def test_dbdd_ppred(n, m, q, D_e, D_s, nb_hints, hint_weight): | |||||
| A, b, dbdd = initialize_from_LWE_instance(DBDD, n, q, m, | |||||
| D_e, D_s, | |||||
| verbosity=2) | |||||
| dbdd_p = DBDD_predict(dbdd.B, matrix(RR, dbdd.S), dbdd.u, verbosity=2) | |||||
| hw = hint_weight | |||||
| if hw == 1: | |||||
| dbdd_d = DBDD_predict_diag( | |||||
| dbdd.B, matrix(RR, dbdd.S), dbdd.u, verbosity=2) | |||||
| d = n + m | |||||
| dbdd.estimate_attack() | |||||
| dbdd_p.estimate_attack() | |||||
| check_all_equal(dbdd, dbdd_p) | |||||
| print("Ok so far.") | |||||
| for h in range(nb_hints): | |||||
| v = vec(d * [0]) | |||||
| for w in range(hint_weight): | |||||
| p = randint(0, d - 1) | |||||
| v[0, p] = randint(- 1, 1) if w < hint_weight - 1 else 1 | |||||
| try: | |||||
| leak = dbdd.leak(v) | |||||
| force = bool(randint(0, 1)) | |||||
| if (h % 3) == 0: | |||||
| dbdd.integrate_perfect_hint(v, leak, | |||||
| non_primitive_action="fail", | |||||
| force=force, | |||||
| catch_invalid_hint=False) | |||||
| dbdd_p.integrate_perfect_hint(v, leak, force=force) | |||||
| if hw == 1: | |||||
| dbdd_d.integrate_perfect_hint(v, leak, force=force) | |||||
| elif (h % 3) == 1: | |||||
| k = randint(2, 12) | |||||
| opt = True # bool(randint(0, 1)) | |||||
| dbdd.integrate_modular_hint(v, leak % k, k, | |||||
| smooth=True, | |||||
| non_primitive_action="fail", | |||||
| force=force, | |||||
| catch_invalid_hint=False) | |||||
| dbdd_p.integrate_modular_hint(v, leak % k, k, | |||||
| smooth=True, | |||||
| force=force) | |||||
| if hw == 1: | |||||
| dbdd_d.integrate_modular_hint(v, leak % k, k, | |||||
| smooth=True, | |||||
| force=force) | |||||
| else: | |||||
| sigma = randint(1, 10) / 10 | |||||
| apost = bool(randint(0, 1)) | |||||
| dbdd.integrate_approx_hint(v, leak, sigma, | |||||
| aposteriori=apost, | |||||
| force=force, | |||||
| catch_invalid_hint=False) | |||||
| dbdd_p.integrate_approx_hint(v, leak, sigma, | |||||
| aposteriori=apost, | |||||
| force=force) | |||||
| if hw == 1: | |||||
| dbdd_d.integrate_approx_hint(v, leak, sigma, | |||||
| aposteriori=apost, | |||||
| force=force) | |||||
| except InvalidHint as e: | |||||
| logging(str(e) + " Skipping both real and predict. \n", | |||||
| style="REJECT") | |||||
| pass | |||||
| dbdd.estimate_attack(silent=True) | |||||
| dbdd_p.estimate_attack(silent=True) | |||||
| if hw == 1: | |||||
| dbdd_d.estimate_attack(silent=True) | |||||
| check_all_equal(dbdd, dbdd_p) | |||||
| if hw == 1: | |||||
| check_all_equal(dbdd, dbdd_d) | |||||
| dbdd.integrate_q_vectors(q) | |||||
| dbdd_p.integrate_q_vectors(q) | |||||
| check_all_equal(dbdd, dbdd_p) | |||||
| if hw == 1: | |||||
| dbdd_d.integrate_q_vectors(q) | |||||
| check_all_equal(dbdd, dbdd_d) | |||||
| dbdd.estimate_attack() | |||||
| dbdd_p.estimate_attack() | |||||
| if hw == 1: | |||||
| dbdd_d.estimate_attack() | |||||
| dbdd.attack() | |||||
| logging("Passed that batch of tests !", style="SUCCESS") | |||||
| def random_PSD(d, variance, repeat=5, diag=False): | |||||
| S = matrix(d * [d * [0]]) | |||||
| noise = vec(d * [0]) | |||||
| for x in range(repeat * d): | |||||
| if not diag: | |||||
| V = vec([randint(- 10, 10) + randint(- 10, 10) for i in range(d)]) | |||||
| else: | |||||
| V = vec(d * [0]) | |||||
| V[0, randint(0, d - 1)] = 1 | |||||
| f = (variance / (repeat * scal(V * V.T))) | |||||
| S += f * V.T * V | |||||
| noise += round_to_rational(gauss(0, sqrt(f))) * V | |||||
| return S, noise | |||||
| def test_dbdd_ppred_fulldimapprox(n, m, q, D_e, D_s, nb_hints, diag=False): | |||||
| A, b, dbdd = initialize_from_LWE_instance(DBDD, | |||||
| n, q, | |||||
| m, D_e, | |||||
| D_s, | |||||
| verbosity=2) | |||||
| dbdd_p = DBDD_predict(dbdd.B, matrix(RR, dbdd.S), dbdd.u, verbosity=2) | |||||
| if diag: | |||||
| dbdd_d = DBDD_predict_diag(dbdd.B, matrix(RR, dbdd.S), | |||||
| dbdd.u, verbosity=2) | |||||
| d = n + m | |||||
| dbdd.estimate_attack() | |||||
| dbdd_p.estimate_attack() | |||||
| check_all_equal(dbdd, dbdd_p) | |||||
| if diag: | |||||
| dbdd_d.estimate_attack() | |||||
| check_all_equal(dbdd, dbdd_d) | |||||
| for h in range(nb_hints): | |||||
| S, noise = random_PSD(d, 10, repeat=10, diag=diag) | |||||
| dbdd.integrate_approx_hint_fulldim(dbdd.u[:, :-1] + noise, S) | |||||
| dbdd_p.integrate_approx_hint_fulldim(None, S) | |||||
| if diag: | |||||
| dbdd_d.integrate_approx_hint_fulldim(None, S) | |||||
| dbdd.estimate_attack() | |||||
| dbdd_p.estimate_attack() | |||||
| check_all_equal(dbdd, dbdd_p) | |||||
| if diag: | |||||
| dbdd_d.estimate_attack() | |||||
| check_all_equal(dbdd, dbdd_d) | |||||
| dbdd.attack() | |||||
| logging("Passed that batch of tests !", style="SUCCESS") | |||||
| """ | |||||
| Starting the tests | |||||
| """ | |||||
| n = 8 | |||||
| m = 16 | |||||
| q = 90 # 2 ** 13 | |||||
| D_s = build_centered_binomial_law(4) | |||||
| D_e = build_centered_binomial_law(4) | |||||
| test_dbdd_ppred_fulldimapprox(n, m, q, D_e, D_s, 3, diag=True) | |||||
| test_dbdd_ppred_fulldimapprox(n, m, q, D_e, D_s, 3) | |||||
| n = 8 | |||||
| m = 16 | |||||
| q = 90 # 2 ** 13 | |||||
| D_s = build_centered_binomial_law(3) | |||||
| D_e = build_centered_binomial_law(5) | |||||
| test_dbdd_ppred_fulldimapprox(n, m, q, D_e, D_s, 3, diag=True) | |||||
| test_dbdd_ppred_fulldimapprox(n, m, q, D_e, D_s, 3) | |||||
| n = 30 | |||||
| m = 45 | |||||
| q = 90 # 2 ** 13 | |||||
| D_s = build_centered_binomial_law(4) | |||||
| D_e = build_centered_binomial_law(4) | |||||
| test_dbdd_ppred(n, m, q, D_e, D_s, 40, 1) | |||||
| test_dbdd_ppred(n, m, q, D_e, D_s, 40, 2) | |||||
| test_dbdd_ppred(n, m, q, D_e, D_s, 40, 3) | |||||
| D_s = build_centered_binomial_law(3) | |||||
| D_e = build_centered_binomial_law(5) | |||||
| test_dbdd_ppred(n, m, q, D_e, D_s, 40, 1) | |||||
| test_dbdd_ppred(n, m, q, D_e, D_s, 40, 2) | |||||
| test_dbdd_ppred(n, m, q, D_e, D_s, 40, 3) | |||||
| logging("All test pass !", style="SUCCESS") |
+ 86
- 0
Sec5.2_validation/compare_usvp_models.sage
Прегледај датотеку
| from multiprocessing import Pool | |||||
| from map_drop import map_drop | |||||
| from numpy.random import seed as np_seed | |||||
| load("../framework/instance_gen.sage") | |||||
| Derr = build_centered_binomial_law(6) | |||||
| modulus = 11 | |||||
| try: | |||||
| N_tests = int(sys.argv[1]) | |||||
| threads = int(sys.argv[2]) | |||||
| except: | |||||
| N_tests = 5 | |||||
| threads = 1 | |||||
| def v(i): | |||||
| return canonical_vec(d, i) | |||||
| def randv(): | |||||
| vv = v(randint(0, d - 1)) | |||||
| vv -= v(randint(0, d - 1)) | |||||
| vv += v(randint(0, d - 1)) | |||||
| vv -= v(randint(0, d - 1)) | |||||
| vv += v(randint(0, d - 1)) | |||||
| return vv | |||||
| def one_experiment(id, aargs): | |||||
| N_hints, T_hints, simul, probabilistic = aargs | |||||
| mu, variance = average_variance(Derr) | |||||
| set_random_seed(id) | |||||
| np_seed(seed=id) | |||||
| A, b, dbdd = initialize_from_LWE_instance(DBDD_predict if simul else DBDD, | |||||
| n, q, m, D_e, D_s, verbosity=0) | |||||
| if simul: | |||||
| beta, _ = dbdd.estimate_attack(tours=1, probabilistic=probabilistic) | |||||
| return beta | |||||
| else: | |||||
| beta, _ = dbdd.attack(tours=1) | |||||
| return beta | |||||
| dic = {" ": None} | |||||
| def validation_prediction(N_tests, N_hints, T_hints): | |||||
| # Estimation | |||||
| import datetime | |||||
| ttt = datetime.datetime.now() | |||||
| pred_N_test = int(ceil(threads / 2)) | |||||
| res = map_drop(pred_N_test, pred_N_test, one_experiment, | |||||
| (N_hints, T_hints, True, True)) | |||||
| beta_pred_proba = RR(sum(res)) / (pred_N_test) | |||||
| res = map_drop(pred_N_test, pred_N_test, one_experiment, | |||||
| (N_hints, T_hints, True, False)) | |||||
| beta_pred_intersect = RR(sum(res)) / (pred_N_test) | |||||
| res = map_drop(N_tests, threads, one_experiment, | |||||
| (N_hints, T_hints, False, None)) | |||||
| beta_real = RR(sum(res)) / N_tests | |||||
| print("n:%3d Beta Real: %2.3f Beta predicted: %2.3f beta predicted(intersect): %2.3f " | |||||
| % (n, beta_real, beta_pred_proba, beta_pred_intersect), end=" \t") | |||||
| print("Walltime: ", datetime.datetime.now() - ttt, end=" \t") | |||||
| print("DIFF \t\t%.3f,\t%.3f,\t%.3f" | |||||
| % (beta_real, beta_pred_proba - beta_real, | |||||
| beta_pred_intersect - beta_real)) | |||||
| return | |||||
| logging("Number of threads : %d" % threads, style="DATA") | |||||
| logging("Number of Samples : %d" % N_tests, style="DATA") | |||||
| logging(" Validation tests ", style="HEADER") | |||||
| for k in range(30, 100, 2): | |||||
| n = k | |||||
| m = n | |||||
| q = 3301 | |||||
| D_s = build_centered_binomial_law(40) | |||||
| D_e = build_centered_binomial_law(40) | |||||
| d = m + n | |||||
| validation_prediction(N_tests, 0, "None") # Line 0 |
BIN
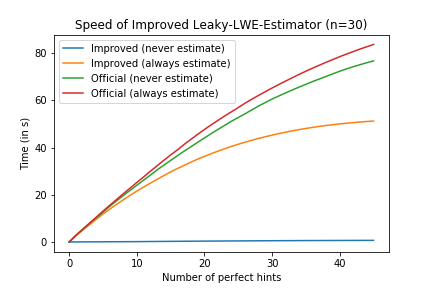
Sec5.2_validation/comparison-speed.png
Прегледај датотеку
+ 46
- 0
Sec5.2_validation/map_drop.py
Прегледај датотеку
| import time | |||||
| from multiprocessing import Process, Queue | |||||
| return_queue = Queue() | |||||
| def test_process(i, return_queue): | |||||
| time.sleep(4 * i + 1) | |||||
| return_queue.put(3 * i + 2) | |||||
| def map_drop(nb, threads, f, aargs, max_drop=0): | |||||
| processes = [] | |||||
| def ff(i, args, return_queue): | |||||
| for trial in range(10): | |||||
| r = f(i + 2**16 * trial, args) | |||||
| return_queue.put(r) | |||||
| return | |||||
| # except: | |||||
| # pass | |||||
| # print "FAILED 10 TIMES" | |||||
| for i in range(threads): | |||||
| process = Process(target=ff, args=(i, aargs, return_queue)) | |||||
| processes.append(process) | |||||
| process.start() | |||||
| ret = [] | |||||
| for i in range(threads, nb + threads): | |||||
| ret.append(return_queue.get()) # this is blocking | |||||
| if len(ret) == nb: | |||||
| break | |||||
| if i < nb + max_drop: | |||||
| process = Process(target=ff, args=(i, aargs, return_queue)) | |||||
| processes.append(process) | |||||
| process.start() | |||||
| for process in processes: | |||||
| if process.is_alive(): | |||||
| process.terminate() | |||||
| if len(ret) != nb: | |||||
| print(len(ret), nb) | |||||
| raise ValueError("Something went wrong.") | |||||
| return ret |
+ 154
- 0
Sec5.2_validation/prediction_verifications.sage
Прегледај датотеку
| from multiprocessing import Pool | |||||
| from map_drop import map_drop | |||||
| from numpy.random import seed as np_seed | |||||
| load("../framework/instance_gen.sage") | |||||
| Derr = build_centered_binomial_law(6) | |||||
| modulus = 11 | |||||
| saving_results = True | |||||
| try: | |||||
| N_tests = int(sys.argv[1]) | |||||
| threads = int(sys.argv[2]) | |||||
| except: | |||||
| N_tests = 5 | |||||
| threads = 1 | |||||
| def v(i): | |||||
| return canonical_vec(d, i) | |||||
| qvec_donttouch = 20 | |||||
| def randv(): | |||||
| vv = v(randint(qvec_donttouch, d - 1)) | |||||
| vv -= v(randint(qvec_donttouch, d - 1)) | |||||
| vv += v(randint(qvec_donttouch, d - 1)) | |||||
| vv -= v(randint(qvec_donttouch, d - 1)) | |||||
| vv += v(randint(qvec_donttouch, d - 1)) | |||||
| return vv | |||||
| def one_experiment(id, aargs): | |||||
| (N_hints, T_hints) = aargs | |||||
| mu, variance = average_variance(Derr) | |||||
| set_random_seed(id) | |||||
| np_seed(seed=id) | |||||
| A, b, dbdd = initialize_from_LWE_instance(DBDD, n, q, | |||||
| m, D_e, D_s, | |||||
| verbosity=0) | |||||
| A, b, dbdd_p = initialize_from_LWE_instance(DBDD_predict, | |||||
| n, q, m, D_e, | |||||
| D_s, | |||||
| verbosity=0) | |||||
| for j in range(N_hints): | |||||
| vv = randv() | |||||
| print(vv) | |||||
| if T_hints == "Perfect": | |||||
| dbdd.integrate_perfect_hint(vv, dbdd.leak(vv), estimate=False) | |||||
| dbdd_p.integrate_perfect_hint(vv, dbdd_p.leak(vv), estimate=False) | |||||
| if T_hints == "Approx": | |||||
| dbdd.integrate_approx_hint(vv, dbdd.leak(vv) + | |||||
| draw_from_distribution(Derr), | |||||
| variance, estimate=False) | |||||
| dbdd_p.integrate_approx_hint(vv, dbdd_p.leak(vv) + | |||||
| draw_from_distribution(Derr), | |||||
| variance, estimate=False) | |||||
| if T_hints == "Modular": | |||||
| dbdd.integrate_modular_hint(vv, dbdd.leak(vv) % modulus, | |||||
| modulus, smooth=True, estimate=False) | |||||
| dbdd_p.integrate_modular_hint(vv, dbdd_p.leak(vv) % modulus, | |||||
| modulus, smooth=True, estimate=False) | |||||
| if T_hints == "Q-Modular": | |||||
| dbdd.integrate_q_modular_hint(vv, dbdd.leak(vv) % q, | |||||
| q, estimate=False) | |||||
| dbdd_p.integrate_q_modular_hint(vv, dbdd_p.leak(vv) % modulus, | |||||
| q, estimate=False) | |||||
| dbdd_p.integrate_q_vectors(q, indices=range(20)) | |||||
| dbdd.integrate_q_vectors(q, indices=range(20)) | |||||
| beta_pred_light, _ = dbdd_p.estimate_attack(probabilistic=True) | |||||
| beta_pred_full, _ = dbdd.estimate_attack(probabilistic=True) | |||||
| beta, _ = dbdd.attack() | |||||
| return (beta, beta_pred_full, beta_pred_light) | |||||
| dic = {" ": None} | |||||
| def validation_prediction(N_tests, N_hints, T_hints): | |||||
| # Estimation | |||||
| import datetime | |||||
| ttt = datetime.datetime.now() | |||||
| res = map_drop(N_tests, threads, one_experiment, (N_hints, T_hints)) | |||||
| beta_real = RR(sum([r[0] for r in res])) / N_tests | |||||
| beta_pred_full = RR(sum([r[1] for r in res])) / N_tests | |||||
| beta_pred_light = RR(sum([r[2] for r in res])) / N_tests | |||||
| print("%d,\t %.3f,\t %.3f,\t %.3f \t\t" % | |||||
| (N_hints, beta_real, beta_pred_full, beta_pred_light), end=" \t") | |||||
| print("Time:", datetime.datetime.now() - ttt) | |||||
| if saving_results: | |||||
| vbeta_real = RR(sum([r[0]**2 for r in res])) / N_tests - beta_real | |||||
| beta_pred_full = RR(sum([r[0]**2 for r in res])) / N_tests - beta_pred_full | |||||
| beta_pred_light = RR(sum([r[0]**2 for r in res])) / N_tests - beta_pred_light | |||||
| with open('results.csv') as _file: | |||||
| _file.write(f'{T_hints};{N_hints};{N_tests};{datetime.datetime.now() - ttt};') | |||||
| _file.write(f'{beta_real};{beta_pred_full};{beta_pred_light};') | |||||
| _file.write(f'{vbeta_real};{vbeta_pred_full};{vbeta_pred_light};') | |||||
| _file.write(f'\n') | |||||
| return beta_pred_full | |||||
| logging("Number of threads : %d" % threads, style="DATA") | |||||
| logging("Number of Samples : %d" % N_tests, style="DATA") | |||||
| logging(" Validation tests ", style="HEADER") | |||||
| n = 70 | |||||
| m = n | |||||
| q = 3301 | |||||
| D_s = build_centered_binomial_law(40) | |||||
| D_e = build_centered_binomial_law(40) | |||||
| d = m + n | |||||
| print("\n \n None") | |||||
| print("hints,\t real,\t pred_full, \t pred_light,") | |||||
| beta_pred = validation_prediction(N_tests, 0, "None") | |||||
| print("\n \n Perfect") | |||||
| print("hints,\t real,\t pred_full, \t pred_light,") | |||||
| for h in range(1, 100): | |||||
| beta_pred = validation_prediction(N_tests, h, "Perfect") # Line 0 | |||||
| if beta_pred < 3: | |||||
| break | |||||
| print("\n \n Modular") | |||||
| print("hints,\t real,\t pred_full, \t pred_light,") | |||||
| for h in range(2, 200, 2): | |||||
| beta_pred = validation_prediction(N_tests, h, "Modular") # Line 0 | |||||
| if beta_pred < 3: | |||||
| break | |||||
| print("\n \n Approx") | |||||
| print("hints,\t real,\t pred_full, \t pred_light,") | |||||
| for h in range(4, 200, 4): | |||||
| beta_pred = validation_prediction(N_tests, h, "Approx") # Line 0 | |||||
| if beta_pred < 3: | |||||
| break | |||||
| print("\n \n Q-Modular") | |||||
| print("hints,\t real,\t pred_full, \t pred_light,") | |||||
| for h in range(1, 100): | |||||
| beta_pred = validation_prediction(N_tests, h, "Q-Modular") # Line 0 | |||||
| if beta_pred < 3: | |||||
| break |
+ 161
- 0
Sec5.2_validation/time_verifications.sage
Прегледај датотеку
| from multiprocessing import Pool | |||||
| from map_drop import map_drop | |||||
| from numpy.random import seed as np_seed | |||||
| import time | |||||
| load("../framework/instance_gen.sage") | |||||
| Derr = build_centered_binomial_law(6) | |||||
| modulus = 11 | |||||
| try: | |||||
| N_tests = int(sys.argv[1]) | |||||
| threads = int(sys.argv[2]) | |||||
| except: | |||||
| N_tests = 5 | |||||
| threads = 1 | |||||
| def v(i): | |||||
| return canonical_vec(d, i) | |||||
| qvec_donttouch = 35 | |||||
| def randv(): | |||||
| vv = v(randint(qvec_donttouch, d - 1)) | |||||
| vv -= v(randint(qvec_donttouch, d - 1)) | |||||
| vv += v(randint(qvec_donttouch, d - 1)) | |||||
| vv -= v(randint(qvec_donttouch, d - 1)) | |||||
| vv += v(randint(qvec_donttouch, d - 1)) | |||||
| return vv | |||||
| def one_experiment(id, aargs): | |||||
| (N_hints, T_hints) = aargs | |||||
| mu, variance = average_variance(Derr) | |||||
| set_random_seed(id) | |||||
| np_seed(seed=id) | |||||
| A, b, dbdd1 = initialize_from_LWE_instance(DBDD, n, q, | |||||
| m, D_e, D_s, | |||||
| verbosity=0) | |||||
| A, b, dbdd2 = initialize_from_LWE_instance(DBDD, | |||||
| n, q, m, D_e, | |||||
| D_s, | |||||
| verbosity=0) | |||||
| dbdd1._keep_basis = False | |||||
| dbdd2._keep_basis = True | |||||
| dbdd1_time = 0. | |||||
| dbdd2_time = 0. | |||||
| for j in range(N_hints): | |||||
| vv = randv() | |||||
| ##print(vv) | |||||
| if T_hints == "Perfect": | |||||
| start_time = time.time() | |||||
| dbdd1.integrate_perfect_hint(vv, dbdd1.leak(vv), estimate=False) | |||||
| middle_time = time.time() | |||||
| dbdd2.integrate_perfect_hint(vv, dbdd2.leak(vv), estimate=False) | |||||
| end_time = time.time() | |||||
| if T_hints == "Approx": | |||||
| start_time = time.time() | |||||
| dbdd1.integrate_approx_hint(vv, dbdd1.leak(vv) + | |||||
| draw_from_distribution(Derr), | |||||
| variance, estimate=False) | |||||
| middle_time = time.time() | |||||
| dbdd2.integrate_approx_hint(vv, dbdd2.leak(vv) + | |||||
| draw_from_distribution(Derr), | |||||
| variance, estimate=False) | |||||
| end_time = time.time() | |||||
| if T_hints == "Modular": | |||||
| start_time = time.time() | |||||
| dbdd1.integrate_modular_hint(vv, dbdd1.leak(vv) % modulus, | |||||
| modulus, smooth=True, estimate=False) | |||||
| middle_time = time.time() | |||||
| dbdd2.integrate_modular_hint(vv, dbdd2.leak(vv) % modulus, | |||||
| modulus, smooth=True, estimate=False) | |||||
| end_time = time.time() | |||||
| dbdd1_time += middle_time - start_time | |||||
| dbdd2_time += end_time - middle_time | |||||
| print('q-vectors') | |||||
| start_time = time.time() | |||||
| dbdd1.integrate_q_vectors(q, indices=range(35)) | |||||
| beta_pred_1, _ = dbdd1.estimate_attack(probabilistic=True) | |||||
| beta1, _ = dbdd1.attack() | |||||
| middle_time = time.time() | |||||
| dbdd2.integrate_q_vectors(q, indices=range(35)) | |||||
| beta_pred_2, _ = dbdd2.estimate_attack(probabilistic=True) | |||||
| beta2, _ = dbdd2.attack() | |||||
| end_time = time.time() | |||||
| dbdd1_time += middle_time - start_time | |||||
| dbdd2_time += end_time - middle_time | |||||
| return (beta, beta1, beta2, dbdd1_time, dbdd2_time) | |||||
| dic = {" ": None} | |||||
| def validation_prediction(N_tests, N_hints, T_hints): | |||||
| # Estimation | |||||
| import datetime | |||||
| ttt = datetime.datetime.now() | |||||
| res = map_drop(N_tests, threads, one_experiment, (N_hints, T_hints)) | |||||
| beta_real = RR(sum([r[0] for r in res])) / N_tests | |||||
| beta_pred_full = RR(sum([r[1] for r in res])) / N_tests | |||||
| beta_pred_light = RR(sum([r[2] for r in res])) / N_tests | |||||
| dbdd1_time = RR(sum([r[3] for r in res])) / N_tests | |||||
| dbdd2_time = RR(sum([r[4] for r in res])) / N_tests | |||||
| print("%d,\t %.3f,\t %.3f,\t %.3f,\t %.3f,\t %.3f \t\t" % | |||||
| (N_hints, beta_real, beta_pred_full, beta_pred_light, dbdd1_time, dbdd2_time), end=" \t") | |||||
| print("Time:", datetime.datetime.now() - ttt) | |||||
| return beta_pred_full | |||||
| logging("Number of threads : %d" % threads, style="DATA") | |||||
| logging("Number of Samples : %d" % N_tests, style="DATA") | |||||
| logging(" Validation tests ", style="HEADER") | |||||
| n = 70 | |||||
| m = n | |||||
| q = 3301 | |||||
| D_s = build_centered_binomial_law(40) | |||||
| D_e = build_centered_binomial_law(40) | |||||
| d = m + n | |||||
| #print("\n \n None") | |||||
| #print("hints,\t real,\t pred_full, \t pred_light,") | |||||
| #beta_pred = validation_prediction(N_tests, 0, "None") | |||||
| print("\n \n Perfect") | |||||
| print("hints,\t real,\t pred_full, \t pred_light,") | |||||
| for h in range(2, 100): | |||||
| beta_pred = validation_prediction(N_tests, h, "Perfect") # Line 0 | |||||
| if beta_pred < 3: | |||||
| break | |||||
| print("\n \n Modular") | |||||
| print("hints,\t real,\t pred_full, \t pred_light,") | |||||
| for h in range(2, 200, 2): | |||||
| beta_pred = validation_prediction(N_tests, h, "Modular") # Line 0 | |||||
| if beta_pred < 3: | |||||
| break | |||||
| print("\n \n Approx") | |||||
| print("hints,\t real,\t pred_full, \t pred_light,") | |||||
| for h in range(4, 200, 4): | |||||
| beta_pred = validation_prediction(N_tests, h, "Approx") # Line 0 | |||||
| if beta_pred < 3: | |||||
| break |
+ 1460
- 0
Sec6_applications/.ipynb_checkpoints/LWE with Side Information-checkpoint.ipynb
Разлика између датотеке није приказан због своје велике величине
Прегледај датотеку
+ 6
- 0
Sec6_applications/.ipynb_checkpoints/TEST-checkpoint.ipynb
Прегледај датотеку
| { | |||||
| "cells": [], | |||||
| "metadata": {}, | |||||
| "nbformat": 4, | |||||
| "nbformat_minor": 2 | |||||
| } |
+ 30
- 0
Sec6_applications/Frodo_Single_data/aposteriori_distribution_CCS1.sage
Прегледај датотеку
| variance_aposteriori = {} | |||||
| center_aposteriori = {} | |||||
| proba_best_guess_correct = {} | |||||
| nb_samples_for_measure = 9720 | |||||
| variance_aposteriori[0] = 0.015568292051926624 | |||||
| center_aposteriori[0] = 0.008436213991769548 | |||||
| proba_best_guess_correct[0] = 0.9951646090534979 | |||||
| nb_samples_for_measure = 7415 | |||||
| variance_aposteriori[1] = 0.1765582091143198 | |||||
| center_aposteriori[1] = 1.2115981119352663 | |||||
| proba_best_guess_correct[1] = 0.7932569116655428 | |||||
| nb_samples_for_measure = 1456 | |||||
| variance_aposteriori[2] = 0.3125410671802424 | |||||
| center_aposteriori[2] = 1.4120879120879122 | |||||
| proba_best_guess_correct[2] = 0.44711538461538464 | |||||
| nb_samples_for_measure = 275 | |||||
| variance_aposteriori[3] = 0.11660252156602527 | |||||
| center_aposteriori[3] = 2.938181818181818 | |||||
| proba_best_guess_correct[3] = 0.9672727272727273 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[-3] = None | |||||
| center_aposteriori[-3] = 0 | |||||
| nb_samples_for_measure = 2367 | |||||
| variance_aposteriori[-2] = 0.117016128715456 | |||||
| center_aposteriori[-2] = -2.0549218419939734 | |||||
| proba_best_guess_correct[-2] = 0.8800168990283058 | |||||
| nb_samples_for_measure = 6927 | |||||
| variance_aposteriori[-1] = 0.0735451983247931 | |||||
| center_aposteriori[-1] = -1.0474953082141383 | |||||
| proba_best_guess_correct[-1] = 0.9666522304027718 |
+ 38
- 0
Sec6_applications/Frodo_Single_data/aposteriori_distribution_CCS2.sage
Прегледај датотеку
| variance_aposteriori = {} | |||||
| center_aposteriori = {} | |||||
| proba_best_guess_correct = {} | |||||
| nb_samples_for_measure = 18205 | |||||
| variance_aposteriori[0] = 0.0009336162751533763 | |||||
| center_aposteriori[0] = 0.0004943696786597089 | |||||
| proba_best_guess_correct[0] = 0.9997253501785224 | |||||
| nb_samples_for_measure = 12051 | |||||
| variance_aposteriori[1] = 0.126514237037542 | |||||
| center_aposteriori[1] = 1.1464608746162144 | |||||
| proba_best_guess_correct[1] = 0.85428595137333 | |||||
| nb_samples_for_measure = 2164 | |||||
| variance_aposteriori[2] = 0.2612093578525752 | |||||
| center_aposteriori[2] = 1.5013863216266174 | |||||
| proba_best_guess_correct[2] = 0.5069316081330869 | |||||
| nb_samples_for_measure = 251 | |||||
| variance_aposteriori[3] = 0.015936254980079674 | |||||
| center_aposteriori[3] = 2.99203187250996 | |||||
| proba_best_guess_correct[3] = 0.9960159362549801 | |||||
| nb_samples_for_measure = 22 | |||||
| variance_aposteriori[4] = 0.0 | |||||
| center_aposteriori[4] = 4.0 | |||||
| proba_best_guess_correct[4] = 1.0 | |||||
| nb_samples_for_measure = 10 | |||||
| variance_aposteriori[-4] = None | |||||
| center_aposteriori[-4] = 0 | |||||
| nb_samples_for_measure = 289 | |||||
| variance_aposteriori[-3] = 0.47750865051903113 | |||||
| center_aposteriori[-3] = -2.449826989619396 | |||||
| proba_best_guess_correct[-3] = 0.5640138408304498 | |||||
| nb_samples_for_measure = 2952 | |||||
| variance_aposteriori[-2] = 0.031682338172077065 | |||||
| center_aposteriori[-2] = -2.029132791327811 | |||||
| proba_best_guess_correct[-2] = 0.9725609756097561 | |||||
| nb_samples_for_measure = 11416 | |||||
| variance_aposteriori[-1] = 0.011268498063594881 | |||||
| center_aposteriori[-1] = -1.005693763139334 | |||||
| proba_best_guess_correct[-1] = 0.9971093202522775 |
+ 46
- 0
Sec6_applications/Frodo_Single_data/aposteriori_distribution_CCS3.sage
Прегледај датотеку
| variance_aposteriori = {} | |||||
| center_aposteriori = {} | |||||
| proba_best_guess_correct = {} | |||||
| nb_samples_for_measure = 17763 | |||||
| variance_aposteriori[0] = 0.0002251871868490683 | |||||
| center_aposteriori[0] = 0.00011259359342453415 | |||||
| proba_best_guess_correct[0] = 0.9999437032032877 | |||||
| nb_samples_for_measure = 14473 | |||||
| variance_aposteriori[1] = 0.16206964097039386 | |||||
| center_aposteriori[1] = 1.2018240862295309 | |||||
| proba_best_guess_correct[1] = 0.7986595729979963 | |||||
| nb_samples_for_measure = 4885 | |||||
| variance_aposteriori[2] = 0.24248937688036967 | |||||
| center_aposteriori[2] = 1.6040941658137156 | |||||
| proba_best_guess_correct[2] = 0.6057318321392017 | |||||
| nb_samples_for_measure = 1530 | |||||
| variance_aposteriori[3] = 0.002614379084967321 | |||||
| center_aposteriori[3] = 2.9986928104575163 | |||||
| proba_best_guess_correct[3] = 0.9993464052287582 | |||||
| nb_samples_for_measure = 215 | |||||
| variance_aposteriori[4] = 0.0 | |||||
| center_aposteriori[4] = 4.0 | |||||
| proba_best_guess_correct[4] = 1.0 | |||||
| nb_samples_for_measure = 17 | |||||
| variance_aposteriori[5] = 0.0 | |||||
| center_aposteriori[5] = 5.0 | |||||
| proba_best_guess_correct[5] = 1.0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[-5] = None | |||||
| center_aposteriori[-5] = 0 | |||||
| nb_samples_for_measure = 238 | |||||
| variance_aposteriori[-4] = 0.08261532461085698 | |||||
| center_aposteriori[-4] = -3.9579831932787783 | |||||
| proba_best_guess_correct[-4] = 0.9789915966386554 | |||||
| nb_samples_for_measure = 703 | |||||
| variance_aposteriori[-3] = 0.533655112602481 | |||||
| center_aposteriori[-3] = -2.102418207679875 | |||||
| proba_best_guess_correct[-3] = 0.2972972972972973 | |||||
| nb_samples_for_measure = 7025 | |||||
| variance_aposteriori[-2] = 0.16290165289926153 | |||||
| center_aposteriori[-2] = -2.1870462633451098 | |||||
| proba_best_guess_correct[-2] = 0.8120996441281139 | |||||
| nb_samples_for_measure = 13311 | |||||
| variance_aposteriori[-1] = 0.030019979182636547 | |||||
| center_aposteriori[-1] = -1.013522650438972 | |||||
| proba_best_guess_correct[-1] = 0.9923371647509579 |
+ 52
- 0
Sec6_applications/Frodo_Single_data/aposteriori_distribution_CCS4.sage
Прегледај датотеку
| variance_aposteriori = {} | |||||
| center_aposteriori = {} | |||||
| proba_best_guess_correct = {} | |||||
| nb_samples_for_measure = 20389 | |||||
| variance_aposteriori[0] = 0.0 | |||||
| center_aposteriori[0] = 0.0 | |||||
| proba_best_guess_correct[0] = 1.0 | |||||
| nb_samples_for_measure = 16774 | |||||
| variance_aposteriori[1] = 0.1555140786733543 | |||||
| center_aposteriori[1] = 1.1904733516155956 | |||||
| proba_best_guess_correct[1] = 0.810182425181829 | |||||
| nb_samples_for_measure = 5818 | |||||
| variance_aposteriori[2] = 0.23350747707685532 | |||||
| center_aposteriori[2] = 1.6350979718116192 | |||||
| proba_best_guess_correct[2] = 0.6359573736679272 | |||||
| nb_samples_for_measure = 1695 | |||||
| variance_aposteriori[3] = 0.0 | |||||
| center_aposteriori[3] = 3.0 | |||||
| proba_best_guess_correct[3] = 1.0 | |||||
| nb_samples_for_measure = 252 | |||||
| variance_aposteriori[4] = 0.06644849174729654 | |||||
| center_aposteriori[4] = 4.035714285714286 | |||||
| proba_best_guess_correct[4] = 0.9801587301587301 | |||||
| nb_samples_for_measure = 32 | |||||
| variance_aposteriori[5] = 0.15725806451612903 | |||||
| center_aposteriori[5] = 5.1875 | |||||
| proba_best_guess_correct[5] = 0.8125 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[6] = None | |||||
| center_aposteriori[6] = 0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[-6] = None | |||||
| center_aposteriori[-6] = 0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[-5] = None | |||||
| center_aposteriori[-5] = 0 | |||||
| nb_samples_for_measure = 259 | |||||
| variance_aposteriori[-4] = 0.2084343479692317 | |||||
| center_aposteriori[-4] = -4.092664092662744 | |||||
| proba_best_guess_correct[-4] = 0.9459459459459459 | |||||
| nb_samples_for_measure = 960 | |||||
| variance_aposteriori[-3] = 0.49543687000347597 | |||||
| center_aposteriori[-3] = -2.1364583333343035 | |||||
| proba_best_guess_correct[-3] = 0.3125 | |||||
| nb_samples_for_measure = 7684 | |||||
| variance_aposteriori[-2] = 0.152297188239102 | |||||
| center_aposteriori[-2] = -2.1828474752728653 | |||||
| proba_best_guess_correct[-2] = 0.8185840707964602 | |||||
| nb_samples_for_measure = 15257 | |||||
| variance_aposteriori[-1] = 0.026134985826994434 | |||||
| center_aposteriori[-1] = -1.0091761158801091 | |||||
| proba_best_guess_correct[-1] = 0.9960018352231762 |
+ 89
- 0
Sec6_applications/Frodo_Single_data/aposteriori_distribution_NIST1.sage
Прегледај датотеку
| variance_aposteriori = {} | |||||
| center_aposteriori = {} | |||||
| proba_best_guess_correct = {} | |||||
| nb_samples_for_measure = 7408 | |||||
| variance_aposteriori[0] = 0.0 | |||||
| center_aposteriori[0] = 0.0 | |||||
| proba_best_guess_correct[0] = 1.0 | |||||
| nb_samples_for_measure = 7270 | |||||
| variance_aposteriori[1] = 0.39877287866565303 | |||||
| center_aposteriori[1] = 1.3210453920220082 | |||||
| proba_best_guess_correct[1] = 0.7074277854195323 | |||||
| nb_samples_for_measure = 5397 | |||||
| variance_aposteriori[2] = 0.7646728895456155 | |||||
| center_aposteriori[2] = 1.7550491013526033 | |||||
| proba_best_guess_correct[2] = 0.6609227348526959 | |||||
| nb_samples_for_measure = 4147 | |||||
| variance_aposteriori[3] = 0.4438010215743634 | |||||
| center_aposteriori[3] = 3.0694477935857245 | |||||
| proba_best_guess_correct[3] = 0.9879430913913673 | |||||
| nb_samples_for_measure = 2645 | |||||
| variance_aposteriori[4] = 0.15862487094938355 | |||||
| center_aposteriori[4] = 4.0903591682419655 | |||||
| proba_best_guess_correct[4] = 0.9478260869565217 | |||||
| nb_samples_for_measure = 1439 | |||||
| variance_aposteriori[5] = 0.4171456572859571 | |||||
| center_aposteriori[5] = 5.376650451702571 | |||||
| proba_best_guess_correct[5] = 0.7143849895760945 | |||||
| nb_samples_for_measure = 822 | |||||
| variance_aposteriori[6] = 0.3112932718096441 | |||||
| center_aposteriori[6] = 5.369829683698297 | |||||
| proba_best_guess_correct[6] = 0.40875912408759124 | |||||
| nb_samples_for_measure = 151 | |||||
| variance_aposteriori[7] = 0.103841059602649 | |||||
| center_aposteriori[7] = 6.947019867549669 | |||||
| proba_best_guess_correct[7] = 0.9735099337748344 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[8] = None | |||||
| center_aposteriori[8] = 0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[9] = None | |||||
| center_aposteriori[9] = 0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[10] = None | |||||
| center_aposteriori[10] = 0 | |||||
| nb_samples_for_measure = 12 | |||||
| variance_aposteriori[11] = 0.0 | |||||
| center_aposteriori[11] = 11.0 | |||||
| proba_best_guess_correct[11] = 1.0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[-11] = None | |||||
| center_aposteriori[-11] = 0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[-10] = None | |||||
| center_aposteriori[-10] = 0 | |||||
| nb_samples_for_measure = 44 | |||||
| variance_aposteriori[-9] = 0.17758985200845662 | |||||
| center_aposteriori[-9] = -9.090909090908099 | |||||
| proba_best_guess_correct[-9] = 0.9545454545454546 | |||||
| nb_samples_for_measure = 107 | |||||
| variance_aposteriori[-8] = 0.0 | |||||
| center_aposteriori[-8] = -8.0 | |||||
| proba_best_guess_correct[-8] = 1.0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[-7] = None | |||||
| center_aposteriori[-7] = 0 | |||||
| nb_samples_for_measure = 19 | |||||
| variance_aposteriori[-6] = 0.8187134502923975 | |||||
| center_aposteriori[-6] = -4.526315789473301 | |||||
| proba_best_guess_correct[-6] = 0.2631578947368421 | |||||
| nb_samples_for_measure = 756 | |||||
| variance_aposteriori[-5] = 3.2116612355022953 | |||||
| center_aposteriori[-5] = -2.693121693122521 | |||||
| proba_best_guess_correct[-5] = 0.3425925925925926 | |||||
| nb_samples_for_measure = 3453 | |||||
| variance_aposteriori[-4] = 1.096952991319621 | |||||
| center_aposteriori[-4] = -4.577179264408187 | |||||
| proba_best_guess_correct[-4] = 0.7306689834926151 | |||||
| nb_samples_for_measure = 3762 | |||||
| variance_aposteriori[-3] = 0.8372461513213554 | |||||
| center_aposteriori[-3] = -2.6610845295072068 | |||||
| proba_best_guess_correct[-3] = 0.4635832004253057 | |||||
| nb_samples_for_measure = 6524 | |||||
| variance_aposteriori[-2] = 0.4357301753461528 | |||||
| center_aposteriori[-2] = -2.419068056406104 | |||||
| proba_best_guess_correct[-2] = 0.6310545677498467 | |||||
| nb_samples_for_measure = 7244 | |||||
| variance_aposteriori[-1] = 1.9916193765179169 | |||||
| center_aposteriori[-1] = -1.5153230259529664 | |||||
| proba_best_guess_correct[-1] = 0.8734124792932082 |
+ 80
- 0
Sec6_applications/Frodo_Single_data/aposteriori_distribution_NIST2.sage
Прегледај датотеку
| variance_aposteriori = {} | |||||
| center_aposteriori = {} | |||||
| proba_best_guess_correct = {} | |||||
| nb_samples_for_measure = 13205 | |||||
| variance_aposteriori[0] = 0.0 | |||||
| center_aposteriori[0] = 0.0 | |||||
| proba_best_guess_correct[0] = 1.0 | |||||
| nb_samples_for_measure = 15203 | |||||
| variance_aposteriori[1] = 0.21798458216693134 | |||||
| center_aposteriori[1] = 1.2924422811287246 | |||||
| proba_best_guess_correct[1] = 0.7091363546668421 | |||||
| nb_samples_for_measure = 6352 | |||||
| variance_aposteriori[2] = 0.3064210320911798 | |||||
| center_aposteriori[2] = 1.8000629722921915 | |||||
| proba_best_guess_correct[2] = 0.7762909319899244 | |||||
| nb_samples_for_measure = 5910 | |||||
| variance_aposteriori[3] = 0.16892755007632676 | |||||
| center_aposteriori[3] = 3.0253807106598987 | |||||
| proba_best_guess_correct[3] = 0.9956006768189509 | |||||
| nb_samples_for_measure = 3060 | |||||
| variance_aposteriori[4] = 0.027589327111470077 | |||||
| center_aposteriori[4] = 4.014052287581699 | |||||
| proba_best_guess_correct[4] = 0.9928104575163399 | |||||
| nb_samples_for_measure = 1364 | |||||
| variance_aposteriori[5] = 0.24318176439327602 | |||||
| center_aposteriori[5] = 5.2353372434017595 | |||||
| proba_best_guess_correct[5] = 0.7961876832844574 | |||||
| nb_samples_for_measure = 524 | |||||
| variance_aposteriori[6] = 0.3345350517420052 | |||||
| center_aposteriori[6] = 5.412213740458015 | |||||
| proba_best_guess_correct[6] = 0.4580152671755725 | |||||
| nb_samples_for_measure = 101 | |||||
| variance_aposteriori[7] = 0.07841584158415837 | |||||
| center_aposteriori[7] = 6.96039603960396 | |||||
| proba_best_guess_correct[7] = 0.9801980198019802 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[8] = None | |||||
| center_aposteriori[8] = 0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[9] = None | |||||
| center_aposteriori[9] = 0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[10] = None | |||||
| center_aposteriori[10] = 0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[-10] = None | |||||
| center_aposteriori[-10] = 0 | |||||
| nb_samples_for_measure = 12 | |||||
| variance_aposteriori[-9] = 0.0 | |||||
| center_aposteriori[-9] = -9.0 | |||||
| proba_best_guess_correct[-9] = 1.0 | |||||
| nb_samples_for_measure = 43 | |||||
| variance_aposteriori[-8] = 0.0 | |||||
| center_aposteriori[-8] = -8.0 | |||||
| proba_best_guess_correct[-8] = 1.0 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[-7] = None | |||||
| center_aposteriori[-7] = 0 | |||||
| nb_samples_for_measure = 2 | |||||
| variance_aposteriori[-6] = None | |||||
| center_aposteriori[-6] = 0 | |||||
| nb_samples_for_measure = 1639 | |||||
| variance_aposteriori[-5] = 3.5637539194586174 | |||||
| center_aposteriori[-5] = -2.611348383157747 | |||||
| proba_best_guess_correct[-5] = 0.3776693105552166 | |||||
| nb_samples_for_measure = 3598 | |||||
| variance_aposteriori[-4] = 0.658169452247202 | |||||
| center_aposteriori[-4] = -4.334908282377 | |||||
| proba_best_guess_correct[-4] = 0.8390772651473041 | |||||
| nb_samples_for_measure = 0 | |||||
| variance_aposteriori[-3] = None | |||||
| center_aposteriori[-3] = 0 | |||||
| nb_samples_for_measure = 15289 | |||||
| variance_aposteriori[-2] = 0.39810522738958687 | |||||
| center_aposteriori[-2] = -2.4475766891264357 | |||||
| proba_best_guess_correct[-2] = 0.5968997318333442 | |||||
| nb_samples_for_measure = 11778 | |||||
| variance_aposteriori[-1] = 0.3925327006787841 | |||||
| center_aposteriori[-1] = -1.0894039735067054 | |||||
| proba_best_guess_correct[-1] = 0.978689081338088 |
+ 57
- 0
Sec6_applications/Frodo_Single_data/simulation_distribution_CCS1.sage
Прегледај датотеку
| Dguess = {} | |||||
| Dguess[0] = {} | |||||
| Dguess[0][0] = 9673 | |||||
| Dguess[0][1] = 0 | |||||
| Dguess[0][2] = 51 | |||||
| Dguess[0][3] = 0 | |||||
| Dguess[0][-3] = 0 | |||||
| Dguess[0][-2] = 0 | |||||
| Dguess[0][-1] = 0 | |||||
| Dguess[1] = {} | |||||
| Dguess[1][0] = 12 | |||||
| Dguess[1][1] = 5882 | |||||
| Dguess[1][2] = 754 | |||||
| Dguess[1][3] = 8 | |||||
| Dguess[1][-3] = 0 | |||||
| Dguess[1][-2] = 0 | |||||
| Dguess[1][-1] = 0 | |||||
| Dguess[2] = {} | |||||
| Dguess[2][0] = 35 | |||||
| Dguess[2][1] = 1497 | |||||
| Dguess[2][2] = 651 | |||||
| Dguess[2][3] = 1 | |||||
| Dguess[2][-3] = 0 | |||||
| Dguess[2][-2] = 0 | |||||
| Dguess[2][-1] = 0 | |||||
| Dguess[3] = {} | |||||
| Dguess[3][0] = 0 | |||||
| Dguess[3][1] = 36 | |||||
| Dguess[3][2] = 0 | |||||
| Dguess[3][3] = 266 | |||||
| Dguess[3][-3] = 0 | |||||
| Dguess[3][-2] = 0 | |||||
| Dguess[3][-1] = 0 | |||||
| Dguess[-3] = {} | |||||
| Dguess[-3][0] = 0 | |||||
| Dguess[-3][1] = 0 | |||||
| Dguess[-3][2] = 0 | |||||
| Dguess[-3][3] = 0 | |||||
| Dguess[-3][-3] = 0 | |||||
| Dguess[-3][-2] = 207 | |||||
| Dguess[-3][-1] = 98 | |||||
| Dguess[-2] = {} | |||||
| Dguess[-2][0] = 0 | |||||
| Dguess[-2][1] = 0 | |||||
| Dguess[-2][2] = 0 | |||||
| Dguess[-2][3] = 0 | |||||
| Dguess[-2][-3] = 0 | |||||
| Dguess[-2][-2] = 2083 | |||||
| Dguess[-2][-1] = 133 | |||||
| Dguess[-1] = {} | |||||
| Dguess[-1][0] = 0 | |||||
| Dguess[-1][1] = 0 | |||||
| Dguess[-1][2] = 0 | |||||
| Dguess[-1][3] = 0 | |||||
| Dguess[-1][-3] = 0 | |||||
| Dguess[-1][-2] = 77 | |||||
| Dguess[-1][-1] = 6696 |
+ 91
- 0
Sec6_applications/Frodo_Single_data/simulation_distribution_CCS2.sage
Прегледај датотеку
| Dguess = {} | |||||
| Dguess[0] = {} | |||||
| Dguess[0][0] = 18200 | |||||
| Dguess[0][1] = 0 | |||||
| Dguess[0][2] = 12 | |||||
| Dguess[0][3] = 0 | |||||
| Dguess[0][4] = 0 | |||||
| Dguess[0][-4] = 0 | |||||
| Dguess[0][-3] = 0 | |||||
| Dguess[0][-2] = 0 | |||||
| Dguess[0][-1] = 0 | |||||
| Dguess[1] = {} | |||||
| Dguess[1][0] = 1 | |||||
| Dguess[1][1] = 10295 | |||||
| Dguess[1][2] = 1055 | |||||
| Dguess[1][3] = 1 | |||||
| Dguess[1][4] = 0 | |||||
| Dguess[1][-4] = 0 | |||||
| Dguess[1][-3] = 0 | |||||
| Dguess[1][-2] = 0 | |||||
| Dguess[1][-1] = 0 | |||||
| Dguess[2] = {} | |||||
| Dguess[2][0] = 4 | |||||
| Dguess[2][1] = 1747 | |||||
| Dguess[2][2] = 1097 | |||||
| Dguess[2][3] = 0 | |||||
| Dguess[2][4] = 0 | |||||
| Dguess[2][-4] = 0 | |||||
| Dguess[2][-3] = 0 | |||||
| Dguess[2][-2] = 0 | |||||
| Dguess[2][-1] = 0 | |||||
| Dguess[3] = {} | |||||
| Dguess[3][0] = 0 | |||||
| Dguess[3][1] = 9 | |||||
| Dguess[3][2] = 0 | |||||
| Dguess[3][3] = 250 | |||||
| Dguess[3][4] = 0 | |||||
| Dguess[3][-4] = 0 | |||||
| Dguess[3][-3] = 0 | |||||
| Dguess[3][-2] = 0 | |||||
| Dguess[3][-1] = 0 | |||||
| Dguess[4] = {} | |||||
| Dguess[4][0] = 0 | |||||
| Dguess[4][1] = 0 | |||||
| Dguess[4][2] = 0 | |||||
| Dguess[4][3] = 0 | |||||
| Dguess[4][4] = 22 | |||||
| Dguess[4][-4] = 0 | |||||
| Dguess[4][-3] = 0 | |||||
| Dguess[4][-2] = 0 | |||||
| Dguess[4][-1] = 0 | |||||
| Dguess[-4] = {} | |||||
| Dguess[-4][0] = 0 | |||||
| Dguess[-4][1] = 0 | |||||
| Dguess[-4][2] = 0 | |||||
| Dguess[-4][3] = 0 | |||||
| Dguess[-4][4] = 0 | |||||
| Dguess[-4][-4] = 10 | |||||
| Dguess[-4][-3] = 0 | |||||
| Dguess[-4][-2] = 5 | |||||
| Dguess[-4][-1] = 0 | |||||
| Dguess[-3] = {} | |||||
| Dguess[-3][0] = 0 | |||||
| Dguess[-3][1] = 0 | |||||
| Dguess[-3][2] = 0 | |||||
| Dguess[-3][3] = 0 | |||||
| Dguess[-3][4] = 0 | |||||
| Dguess[-3][-4] = 0 | |||||
| Dguess[-3][-3] = 163 | |||||
| Dguess[-3][-2] = 76 | |||||
| Dguess[-3][-1] = 32 | |||||
| Dguess[-2] = {} | |||||
| Dguess[-2][0] = 0 | |||||
| Dguess[-2][1] = 0 | |||||
| Dguess[-2][2] = 0 | |||||
| Dguess[-2][3] = 0 | |||||
| Dguess[-2][4] = 0 | |||||
| Dguess[-2][-4] = 0 | |||||
| Dguess[-2][-3] = 93 | |||||
| Dguess[-2][-2] = 2871 | |||||
| Dguess[-2][-1] = 1 | |||||
| Dguess[-1] = {} | |||||
| Dguess[-1][0] = 0 | |||||
| Dguess[-1][1] = 0 | |||||
| Dguess[-1][2] = 0 | |||||
| Dguess[-1][3] = 0 | |||||
| Dguess[-1][4] = 0 | |||||
| Dguess[-1][-4] = 0 | |||||
| Dguess[-1][-3] = 33 | |||||
| Dguess[-1][-2] = 0 | |||||
| Dguess[-1][-1] = 11383 |
+ 133
- 0
Sec6_applications/Frodo_Single_data/simulation_distribution_CCS3.sage
Прегледај датотеку
| Dguess = {} | |||||
| Dguess[0] = {} | |||||
| Dguess[0][0] = 17762 | |||||
| Dguess[0][1] = 0 | |||||
| Dguess[0][2] = 8 | |||||
| Dguess[0][3] = 0 | |||||
| Dguess[0][4] = 0 | |||||
| Dguess[0][5] = 0 | |||||
| Dguess[0][-5] = 0 | |||||
| Dguess[0][-4] = 0 | |||||
| Dguess[0][-3] = 0 | |||||
| Dguess[0][-2] = 0 | |||||
| Dguess[0][-1] = 0 | |||||
| Dguess[1] = {} | |||||
| Dguess[1][0] = 0 | |||||
| Dguess[1][1] = 11559 | |||||
| Dguess[1][2] = 1918 | |||||
| Dguess[1][3] = 1 | |||||
| Dguess[1][4] = 0 | |||||
| Dguess[1][5] = 0 | |||||
| Dguess[1][-5] = 0 | |||||
| Dguess[1][-4] = 0 | |||||
| Dguess[1][-3] = 0 | |||||
| Dguess[1][-2] = 0 | |||||
| Dguess[1][-1] = 0 | |||||
| Dguess[2] = {} | |||||
| Dguess[2][0] = 1 | |||||
| Dguess[2][1] = 2907 | |||||
| Dguess[2][2] = 2959 | |||||
| Dguess[2][3] = 0 | |||||
| Dguess[2][4] = 0 | |||||
| Dguess[2][5] = 0 | |||||
| Dguess[2][-5] = 0 | |||||
| Dguess[2][-4] = 0 | |||||
| Dguess[2][-3] = 0 | |||||
| Dguess[2][-2] = 0 | |||||
| Dguess[2][-1] = 0 | |||||
| Dguess[3] = {} | |||||
| Dguess[3][0] = 0 | |||||
| Dguess[3][1] = 7 | |||||
| Dguess[3][2] = 0 | |||||
| Dguess[3][3] = 1529 | |||||
| Dguess[3][4] = 0 | |||||
| Dguess[3][5] = 0 | |||||
| Dguess[3][-5] = 0 | |||||
| Dguess[3][-4] = 0 | |||||
| Dguess[3][-3] = 0 | |||||
| Dguess[3][-2] = 0 | |||||
| Dguess[3][-1] = 0 | |||||
| Dguess[4] = {} | |||||
| Dguess[4][0] = 0 | |||||
| Dguess[4][1] = 0 | |||||
| Dguess[4][2] = 0 | |||||
| Dguess[4][3] = 0 | |||||
| Dguess[4][4] = 215 | |||||
| Dguess[4][5] = 0 | |||||
| Dguess[4][-5] = 0 | |||||
| Dguess[4][-4] = 0 | |||||
| Dguess[4][-3] = 0 | |||||
| Dguess[4][-2] = 0 | |||||
| Dguess[4][-1] = 0 | |||||
| Dguess[5] = {} | |||||
| Dguess[5][0] = 0 | |||||
| Dguess[5][1] = 0 | |||||
| Dguess[5][2] = 0 | |||||
| Dguess[5][3] = 0 | |||||
| Dguess[5][4] = 0 | |||||
| Dguess[5][5] = 17 | |||||
| Dguess[5][-5] = 0 | |||||
| Dguess[5][-4] = 0 | |||||
| Dguess[5][-3] = 0 | |||||
| Dguess[5][-2] = 0 | |||||
| Dguess[5][-1] = 0 | |||||
| Dguess[-5] = {} | |||||
| Dguess[-5][0] = 0 | |||||
| Dguess[-5][1] = 0 | |||||
| Dguess[-5][2] = 0 | |||||
| Dguess[-5][3] = 0 | |||||
| Dguess[-5][4] = 0 | |||||
| Dguess[-5][5] = 0 | |||||
| Dguess[-5][-5] = 0 | |||||
| Dguess[-5][-4] = 0 | |||||
| Dguess[-5][-3] = 3 | |||||
| Dguess[-5][-2] = 2 | |||||
| Dguess[-5][-1] = 11 | |||||
| Dguess[-4] = {} | |||||
| Dguess[-4][0] = 0 | |||||
| Dguess[-4][1] = 0 | |||||
| Dguess[-4][2] = 0 | |||||
| Dguess[-4][3] = 0 | |||||
| Dguess[-4][4] = 0 | |||||
| Dguess[-4][5] = 0 | |||||
| Dguess[-4][-5] = 0 | |||||
| Dguess[-4][-4] = 233 | |||||
| Dguess[-4][-3] = 0 | |||||
| Dguess[-4][-2] = 18 | |||||
| Dguess[-4][-1] = 0 | |||||
| Dguess[-3] = {} | |||||
| Dguess[-3][0] = 0 | |||||
| Dguess[-3][1] = 0 | |||||
| Dguess[-3][2] = 0 | |||||
| Dguess[-3][3] = 0 | |||||
| Dguess[-3][4] = 0 | |||||
| Dguess[-3][5] = 0 | |||||
| Dguess[-3][-5] = 0 | |||||
| Dguess[-3][-4] = 0 | |||||
| Dguess[-3][-3] = 209 | |||||
| Dguess[-3][-2] = 1286 | |||||
| Dguess[-3][-1] = 45 | |||||
| Dguess[-2] = {} | |||||
| Dguess[-2][0] = 0 | |||||
| Dguess[-2][1] = 0 | |||||
| Dguess[-2][2] = 0 | |||||
| Dguess[-2][3] = 0 | |||||
| Dguess[-2][4] = 0 | |||||
| Dguess[-2][5] = 0 | |||||
| Dguess[-2][-5] = 0 | |||||
| Dguess[-2][-4] = 5 | |||||
| Dguess[-2][-3] = 345 | |||||
| Dguess[-2][-2] = 5705 | |||||
| Dguess[-2][-1] = 46 | |||||
| Dguess[-1] = {} | |||||
| Dguess[-1][0] = 0 | |||||
| Dguess[-1][1] = 0 | |||||
| Dguess[-1][2] = 0 | |||||
| Dguess[-1][3] = 0 | |||||
| Dguess[-1][4] = 0 | |||||
| Dguess[-1][5] = 0 | |||||
| Dguess[-1][-5] = 0 | |||||
| Dguess[-1][-4] = 0 | |||||
| Dguess[-1][-3] = 146 | |||||
| Dguess[-1][-2] = 14 | |||||
| Dguess[-1][-1] = 13209 |
+ 183
- 0
Sec6_applications/Frodo_Single_data/simulation_distribution_CCS4.sage
Прегледај датотеку
| Dguess = {} | |||||
| Dguess[0] = {} | |||||
| Dguess[0][0] = 20389 | |||||
| Dguess[0][1] = 0 | |||||
| Dguess[0][2] = 5 | |||||
| Dguess[0][3] = 0 | |||||
| Dguess[0][4] = 0 | |||||
| Dguess[0][5] = 0 | |||||
| Dguess[0][6] = 0 | |||||
| Dguess[0][-6] = 0 | |||||
| Dguess[0][-5] = 0 | |||||
| Dguess[0][-4] = 0 | |||||
| Dguess[0][-3] = 0 | |||||
| Dguess[0][-2] = 0 | |||||
| Dguess[0][-1] = 0 | |||||
| Dguess[1] = {} | |||||
| Dguess[1][0] = 0 | |||||
| Dguess[1][1] = 13590 | |||||
| Dguess[1][2] = 2113 | |||||
| Dguess[1][3] = 0 | |||||
| Dguess[1][4] = 0 | |||||
| Dguess[1][5] = 0 | |||||
| Dguess[1][6] = 0 | |||||
| Dguess[1][-6] = 0 | |||||
| Dguess[1][-5] = 0 | |||||
| Dguess[1][-4] = 0 | |||||
| Dguess[1][-3] = 0 | |||||
| Dguess[1][-2] = 0 | |||||
| Dguess[1][-1] = 0 | |||||
| Dguess[2] = {} | |||||
| Dguess[2][0] = 0 | |||||
| Dguess[2][1] = 3173 | |||||
| Dguess[2][2] = 3700 | |||||
| Dguess[2][3] = 0 | |||||
| Dguess[2][4] = 0 | |||||
| Dguess[2][5] = 0 | |||||
| Dguess[2][6] = 0 | |||||
| Dguess[2][-6] = 0 | |||||
| Dguess[2][-5] = 0 | |||||
| Dguess[2][-4] = 0 | |||||
| Dguess[2][-3] = 0 | |||||
| Dguess[2][-2] = 0 | |||||
| Dguess[2][-1] = 0 | |||||
| Dguess[3] = {} | |||||
| Dguess[3][0] = 0 | |||||
| Dguess[3][1] = 11 | |||||
| Dguess[3][2] = 0 | |||||
| Dguess[3][3] = 1695 | |||||
| Dguess[3][4] = 0 | |||||
| Dguess[3][5] = 0 | |||||
| Dguess[3][6] = 0 | |||||
| Dguess[3][-6] = 0 | |||||
| Dguess[3][-5] = 0 | |||||
| Dguess[3][-4] = 0 | |||||
| Dguess[3][-3] = 0 | |||||
| Dguess[3][-2] = 0 | |||||
| Dguess[3][-1] = 0 | |||||
| Dguess[4] = {} | |||||
| Dguess[4][0] = 0 | |||||
| Dguess[4][1] = 0 | |||||
| Dguess[4][2] = 0 | |||||
| Dguess[4][3] = 0 | |||||
| Dguess[4][4] = 247 | |||||
| Dguess[4][5] = 0 | |||||
| Dguess[4][6] = 0 | |||||
| Dguess[4][-6] = 0 | |||||
| Dguess[4][-5] = 0 | |||||
| Dguess[4][-4] = 0 | |||||
| Dguess[4][-3] = 0 | |||||
| Dguess[4][-2] = 0 | |||||
| Dguess[4][-1] = 0 | |||||
| Dguess[5] = {} | |||||
| Dguess[5][0] = 0 | |||||
| Dguess[5][1] = 0 | |||||
| Dguess[5][2] = 0 | |||||
| Dguess[5][3] = 0 | |||||
| Dguess[5][4] = 1 | |||||
| Dguess[5][5] = 26 | |||||
| Dguess[5][6] = 0 | |||||
| Dguess[5][-6] = 0 | |||||
| Dguess[5][-5] = 0 | |||||
| Dguess[5][-4] = 0 | |||||
| Dguess[5][-3] = 0 | |||||
| Dguess[5][-2] = 0 | |||||
| Dguess[5][-1] = 0 | |||||
| Dguess[6] = {} | |||||
| Dguess[6][0] = 0 | |||||
| Dguess[6][1] = 0 | |||||
| Dguess[6][2] = 0 | |||||
| Dguess[6][3] = 0 | |||||
| Dguess[6][4] = 4 | |||||
| Dguess[6][5] = 6 | |||||
| Dguess[6][6] = 0 | |||||
| Dguess[6][-6] = 0 | |||||
| Dguess[6][-5] = 0 | |||||
| Dguess[6][-4] = 0 | |||||
| Dguess[6][-3] = 0 | |||||
| Dguess[6][-2] = 0 | |||||
| Dguess[6][-1] = 0 | |||||
| Dguess[-6] = {} | |||||
| Dguess[-6][0] = 0 | |||||
| Dguess[-6][1] = 0 | |||||
| Dguess[-6][2] = 0 | |||||
| Dguess[-6][3] = 0 | |||||
| Dguess[-6][4] = 0 | |||||
| Dguess[-6][5] = 0 | |||||
| Dguess[-6][6] = 0 | |||||
| Dguess[-6][-6] = 0 | |||||
| Dguess[-6][-5] = 0 | |||||
| Dguess[-6][-4] = 13 | |||||
| Dguess[-6][-3] = 0 | |||||
| Dguess[-6][-2] = 0 | |||||
| Dguess[-6][-1] = 0 | |||||
| Dguess[-5] = {} | |||||
| Dguess[-5][0] = 0 | |||||
| Dguess[-5][1] = 0 | |||||
| Dguess[-5][2] = 0 | |||||
| Dguess[-5][3] = 0 | |||||
| Dguess[-5][4] = 0 | |||||
| Dguess[-5][5] = 0 | |||||
| Dguess[-5][6] = 0 | |||||
| Dguess[-5][-6] = 0 | |||||
| Dguess[-5][-5] = 0 | |||||
| Dguess[-5][-4] = 0 | |||||
| Dguess[-5][-3] = 2 | |||||
| Dguess[-5][-2] = 0 | |||||
| Dguess[-5][-1] = 17 | |||||
| Dguess[-4] = {} | |||||
| Dguess[-4][0] = 0 | |||||
| Dguess[-4][1] = 0 | |||||
| Dguess[-4][2] = 0 | |||||
| Dguess[-4][3] = 0 | |||||
| Dguess[-4][4] = 0 | |||||
| Dguess[-4][5] = 0 | |||||
| Dguess[-4][6] = 0 | |||||
| Dguess[-4][-6] = 0 | |||||
| Dguess[-4][-5] = 0 | |||||
| Dguess[-4][-4] = 245 | |||||
| Dguess[-4][-3] = 0 | |||||
| Dguess[-4][-2] = 11 | |||||
| Dguess[-4][-1] = 0 | |||||
| Dguess[-3] = {} | |||||
| Dguess[-3][0] = 0 | |||||
| Dguess[-3][1] = 0 | |||||
| Dguess[-3][2] = 0 | |||||
| Dguess[-3][3] = 0 | |||||
| Dguess[-3][4] = 0 | |||||
| Dguess[-3][5] = 0 | |||||
| Dguess[-3][6] = 0 | |||||
| Dguess[-3][-6] = 0 | |||||
| Dguess[-3][-5] = 0 | |||||
| Dguess[-3][-4] = 0 | |||||
| Dguess[-3][-3] = 300 | |||||
| Dguess[-3][-2] = 1383 | |||||
| Dguess[-3][-1] = 28 | |||||
| Dguess[-2] = {} | |||||
| Dguess[-2][0] = 0 | |||||
| Dguess[-2][1] = 0 | |||||
| Dguess[-2][2] = 0 | |||||
| Dguess[-2][3] = 0 | |||||
| Dguess[-2][4] = 0 | |||||
| Dguess[-2][5] = 0 | |||||
| Dguess[-2][6] = 0 | |||||
| Dguess[-2][-6] = 0 | |||||
| Dguess[-2][-5] = 0 | |||||
| Dguess[-2][-4] = 1 | |||||
| Dguess[-2][-3] = 483 | |||||
| Dguess[-2][-2] = 6290 | |||||
| Dguess[-2][-1] = 16 | |||||
| Dguess[-1] = {} | |||||
| Dguess[-1][0] = 0 | |||||
| Dguess[-1][1] = 0 | |||||
| Dguess[-1][2] = 0 | |||||
| Dguess[-1][3] = 0 | |||||
| Dguess[-1][4] = 0 | |||||
| Dguess[-1][5] = 0 | |||||
| Dguess[-1][6] = 0 | |||||
| Dguess[-1][-6] = 0 | |||||
| Dguess[-1][-5] = 0 | |||||
| Dguess[-1][-4] = 0 | |||||
| Dguess[-1][-3] = 175 | |||||
| Dguess[-1][-2] = 0 | |||||
| Dguess[-1][-1] = 15196 |
+ 579
- 0
Sec6_applications/Frodo_Single_data/simulation_distribution_NIST1.sage
Прегледај датотеку
| Dguess = {} | |||||
| Dguess[0] = {} | |||||
| Dguess[0][0] = 7408 | |||||
| Dguess[0][1] = 0 | |||||
| Dguess[0][2] = 10 | |||||
| Dguess[0][3] = 0 | |||||
| Dguess[0][4] = 0 | |||||
| Dguess[0][5] = 0 | |||||
| Dguess[0][6] = 0 | |||||
| Dguess[0][7] = 0 | |||||
| Dguess[0][8] = 0 | |||||
| Dguess[0][9] = 0 | |||||
| Dguess[0][10] = 0 | |||||
| Dguess[0][11] = 0 | |||||
| Dguess[0][-11] = 0 | |||||
| Dguess[0][-10] = 0 | |||||
| Dguess[0][-9] = 0 | |||||
| Dguess[0][-8] = 0 | |||||
| Dguess[0][-7] = 0 | |||||
| Dguess[0][-6] = 0 | |||||
| Dguess[0][-5] = 0 | |||||
| Dguess[0][-4] = 0 | |||||
| Dguess[0][-3] = 0 | |||||
| Dguess[0][-2] = 0 | |||||
| Dguess[0][-1] = 0 | |||||
| Dguess[1] = {} | |||||
| Dguess[1][0] = 0 | |||||
| Dguess[1][1] = 5143 | |||||
| Dguess[1][2] = 1746 | |||||
| Dguess[1][3] = 3 | |||||
| Dguess[1][4] = 0 | |||||
| Dguess[1][5] = 0 | |||||
| Dguess[1][6] = 0 | |||||
| Dguess[1][7] = 0 | |||||
| Dguess[1][8] = 0 | |||||
| Dguess[1][9] = 0 | |||||
| Dguess[1][10] = 0 | |||||
| Dguess[1][11] = 0 | |||||
| Dguess[1][-11] = 0 | |||||
| Dguess[1][-10] = 0 | |||||
| Dguess[1][-9] = 0 | |||||
| Dguess[1][-8] = 0 | |||||
| Dguess[1][-7] = 0 | |||||
| Dguess[1][-6] = 0 | |||||
| Dguess[1][-5] = 0 | |||||
| Dguess[1][-4] = 0 | |||||
| Dguess[1][-3] = 0 | |||||
| Dguess[1][-2] = 0 | |||||
| Dguess[1][-1] = 0 | |||||
| Dguess[2] = {} | |||||
| Dguess[2][0] = 0 | |||||
| Dguess[2][1] = 2070 | |||||
| Dguess[2][2] = 3567 | |||||
| Dguess[2][3] = 0 | |||||
| Dguess[2][4] = 0 | |||||
| Dguess[2][5] = 0 | |||||
| Dguess[2][6] = 0 | |||||
| Dguess[2][7] = 0 | |||||
| Dguess[2][8] = 0 | |||||
| Dguess[2][9] = 0 | |||||
| Dguess[2][10] = 0 | |||||
| Dguess[2][11] = 0 | |||||
| Dguess[2][-11] = 0 | |||||
| Dguess[2][-10] = 0 | |||||
| Dguess[2][-9] = 0 | |||||
| Dguess[2][-8] = 0 | |||||
| Dguess[2][-7] = 0 | |||||
| Dguess[2][-6] = 0 | |||||
| Dguess[2][-5] = 0 | |||||
| Dguess[2][-4] = 0 | |||||
| Dguess[2][-3] = 0 | |||||
| Dguess[2][-2] = 0 | |||||
| Dguess[2][-1] = 0 | |||||
| Dguess[3] = {} | |||||
| Dguess[3][0] = 0 | |||||
| Dguess[3][1] = 27 | |||||
| Dguess[3][2] = 0 | |||||
| Dguess[3][3] = 4097 | |||||
| Dguess[3][4] = 0 | |||||
| Dguess[3][5] = 0 | |||||
| Dguess[3][6] = 0 | |||||
| Dguess[3][7] = 0 | |||||
| Dguess[3][8] = 0 | |||||
| Dguess[3][9] = 0 | |||||
| Dguess[3][10] = 0 | |||||
| Dguess[3][11] = 0 | |||||
| Dguess[3][-11] = 0 | |||||
| Dguess[3][-10] = 0 | |||||
| Dguess[3][-9] = 0 | |||||
| Dguess[3][-8] = 0 | |||||
| Dguess[3][-7] = 0 | |||||
| Dguess[3][-6] = 0 | |||||
| Dguess[3][-5] = 0 | |||||
| Dguess[3][-4] = 0 | |||||
| Dguess[3][-3] = 0 | |||||
| Dguess[3][-2] = 0 | |||||
| Dguess[3][-1] = 0 | |||||
| Dguess[4] = {} | |||||
| Dguess[4][0] = 0 | |||||
| Dguess[4][1] = 0 | |||||
| Dguess[4][2] = 0 | |||||
| Dguess[4][3] = 0 | |||||
| Dguess[4][4] = 2507 | |||||
| Dguess[4][5] = 0 | |||||
| Dguess[4][6] = 32 | |||||
| Dguess[4][7] = 0 | |||||
| Dguess[4][8] = 0 | |||||
| Dguess[4][9] = 0 | |||||
| Dguess[4][10] = 0 | |||||
| Dguess[4][11] = 0 | |||||
| Dguess[4][-11] = 0 | |||||
| Dguess[4][-10] = 0 | |||||
| Dguess[4][-9] = 0 | |||||
| Dguess[4][-8] = 0 | |||||
| Dguess[4][-7] = 0 | |||||
| Dguess[4][-6] = 0 | |||||
| Dguess[4][-5] = 0 | |||||
| Dguess[4][-4] = 0 | |||||
| Dguess[4][-3] = 0 | |||||
| Dguess[4][-2] = 0 | |||||
| Dguess[4][-1] = 0 | |||||
| Dguess[5] = {} | |||||
| Dguess[5][0] = 0 | |||||
| Dguess[5][1] = 0 | |||||
| Dguess[5][2] = 0 | |||||
| Dguess[5][3] = 0 | |||||
| Dguess[5][4] = 37 | |||||
| Dguess[5][5] = 1028 | |||||
| Dguess[5][6] = 454 | |||||
| Dguess[5][7] = 4 | |||||
| Dguess[5][8] = 0 | |||||
| Dguess[5][9] = 0 | |||||
| Dguess[5][10] = 0 | |||||
| Dguess[5][11] = 0 | |||||
| Dguess[5][-11] = 0 | |||||
| Dguess[5][-10] = 0 | |||||
| Dguess[5][-9] = 0 | |||||
| Dguess[5][-8] = 0 | |||||
| Dguess[5][-7] = 0 | |||||
| Dguess[5][-6] = 0 | |||||
| Dguess[5][-5] = 0 | |||||
| Dguess[5][-4] = 0 | |||||
| Dguess[5][-3] = 0 | |||||
| Dguess[5][-2] = 0 | |||||
| Dguess[5][-1] = 0 | |||||
| Dguess[6] = {} | |||||
| Dguess[6][0] = 0 | |||||
| Dguess[6][1] = 0 | |||||
| Dguess[6][2] = 0 | |||||
| Dguess[6][3] = 0 | |||||
| Dguess[6][4] = 101 | |||||
| Dguess[6][5] = 280 | |||||
| Dguess[6][6] = 336 | |||||
| Dguess[6][7] = 0 | |||||
| Dguess[6][8] = 0 | |||||
| Dguess[6][9] = 0 | |||||
| Dguess[6][10] = 0 | |||||
| Dguess[6][11] = 0 | |||||
| Dguess[6][-11] = 0 | |||||
| Dguess[6][-10] = 0 | |||||
| Dguess[6][-9] = 0 | |||||
| Dguess[6][-8] = 0 | |||||
| Dguess[6][-7] = 0 | |||||
| Dguess[6][-6] = 0 | |||||
| Dguess[6][-5] = 0 | |||||
| Dguess[6][-4] = 0 | |||||
| Dguess[6][-3] = 0 | |||||
| Dguess[6][-2] = 0 | |||||
| Dguess[6][-1] = 0 | |||||
| Dguess[7] = {} | |||||
| Dguess[7][0] = 0 | |||||
| Dguess[7][1] = 0 | |||||
| Dguess[7][2] = 0 | |||||
| Dguess[7][3] = 0 | |||||
| Dguess[7][4] = 0 | |||||
| Dguess[7][5] = 131 | |||||
| Dguess[7][6] = 0 | |||||
| Dguess[7][7] = 147 | |||||
| Dguess[7][8] = 0 | |||||
| Dguess[7][9] = 0 | |||||
| Dguess[7][10] = 0 | |||||
| Dguess[7][11] = 0 | |||||
| Dguess[7][-11] = 0 | |||||
| Dguess[7][-10] = 0 | |||||
| Dguess[7][-9] = 0 | |||||
| Dguess[7][-8] = 0 | |||||
| Dguess[7][-7] = 0 | |||||
| Dguess[7][-6] = 0 | |||||
| Dguess[7][-5] = 0 | |||||
| Dguess[7][-4] = 0 | |||||
| Dguess[7][-3] = 0 | |||||
| Dguess[7][-2] = 0 | |||||
| Dguess[7][-1] = 0 | |||||
| Dguess[8] = {} | |||||
| Dguess[8][0] = 0 | |||||
| Dguess[8][1] = 30 | |||||
| Dguess[8][2] = 74 | |||||
| Dguess[8][3] = 0 | |||||
| Dguess[8][4] = 0 | |||||
| Dguess[8][5] = 0 | |||||
| Dguess[8][6] = 0 | |||||
| Dguess[8][7] = 0 | |||||
| Dguess[8][8] = 0 | |||||
| Dguess[8][9] = 0 | |||||
| Dguess[8][10] = 0 | |||||
| Dguess[8][11] = 0 | |||||
| Dguess[8][-11] = 0 | |||||
| Dguess[8][-10] = 0 | |||||
| Dguess[8][-9] = 0 | |||||
| Dguess[8][-8] = 0 | |||||
| Dguess[8][-7] = 0 | |||||
| Dguess[8][-6] = 0 | |||||
| Dguess[8][-5] = 0 | |||||
| Dguess[8][-4] = 0 | |||||
| Dguess[8][-3] = 0 | |||||
| Dguess[8][-2] = 0 | |||||
| Dguess[8][-1] = 0 | |||||
| Dguess[9] = {} | |||||
| Dguess[9][0] = 0 | |||||
| Dguess[9][1] = 0 | |||||
| Dguess[9][2] = 0 | |||||
| Dguess[9][3] = 35 | |||||
| Dguess[9][4] = 0 | |||||
| Dguess[9][5] = 0 | |||||
| Dguess[9][6] = 0 | |||||
| Dguess[9][7] = 0 | |||||
| Dguess[9][8] = 0 | |||||
| Dguess[9][9] = 0 | |||||
| Dguess[9][10] = 0 | |||||
| Dguess[9][11] = 0 | |||||
| Dguess[9][-11] = 0 | |||||
| Dguess[9][-10] = 0 | |||||
| Dguess[9][-9] = 0 | |||||
| Dguess[9][-8] = 0 | |||||
| Dguess[9][-7] = 0 | |||||
| Dguess[9][-6] = 0 | |||||
| Dguess[9][-5] = 0 | |||||
| Dguess[9][-4] = 0 | |||||
| Dguess[9][-3] = 0 | |||||
| Dguess[9][-2] = 0 | |||||
| Dguess[9][-1] = 0 | |||||
| Dguess[10] = {} | |||||
| Dguess[10][0] = 0 | |||||
| Dguess[10][1] = 0 | |||||
| Dguess[10][2] = 0 | |||||
| Dguess[10][3] = 12 | |||||
| Dguess[10][4] = 0 | |||||
| Dguess[10][5] = 0 | |||||
| Dguess[10][6] = 0 | |||||
| Dguess[10][7] = 0 | |||||
| Dguess[10][8] = 0 | |||||
| Dguess[10][9] = 0 | |||||
| Dguess[10][10] = 0 | |||||
| Dguess[10][11] = 0 | |||||
| Dguess[10][-11] = 0 | |||||
| Dguess[10][-10] = 0 | |||||
| Dguess[10][-9] = 0 | |||||
| Dguess[10][-8] = 0 | |||||
| Dguess[10][-7] = 0 | |||||
| Dguess[10][-6] = 0 | |||||
| Dguess[10][-5] = 0 | |||||
| Dguess[10][-4] = 0 | |||||
| Dguess[10][-3] = 0 | |||||
| Dguess[10][-2] = 0 | |||||
| Dguess[10][-1] = 0 | |||||
| Dguess[11] = {} | |||||
| Dguess[11][0] = 0 | |||||
| Dguess[11][1] = 0 | |||||
| Dguess[11][2] = 0 | |||||
| Dguess[11][3] = 0 | |||||
| Dguess[11][4] = 0 | |||||
| Dguess[11][5] = 0 | |||||
| Dguess[11][6] = 0 | |||||
| Dguess[11][7] = 0 | |||||
| Dguess[11][8] = 0 | |||||
| Dguess[11][9] = 0 | |||||
| Dguess[11][10] = 0 | |||||
| Dguess[11][11] = 12 | |||||
| Dguess[11][-11] = 0 | |||||
| Dguess[11][-10] = 0 | |||||
| Dguess[11][-9] = 0 | |||||
| Dguess[11][-8] = 0 | |||||
| Dguess[11][-7] = 0 | |||||
| Dguess[11][-6] = 0 | |||||
| Dguess[11][-5] = 0 | |||||
| Dguess[11][-4] = 0 | |||||
| Dguess[11][-3] = 0 | |||||
| Dguess[11][-2] = 0 | |||||
| Dguess[11][-1] = 0 | |||||
| Dguess[-11] = {} | |||||
| Dguess[-11][0] = 0 | |||||
| Dguess[-11][1] = 0 | |||||
| Dguess[-11][2] = 0 | |||||
| Dguess[-11][3] = 0 | |||||
| Dguess[-11][4] = 0 | |||||
| Dguess[-11][5] = 0 | |||||
| Dguess[-11][6] = 0 | |||||
| Dguess[-11][7] = 0 | |||||
| Dguess[-11][8] = 0 | |||||
| Dguess[-11][9] = 0 | |||||
| Dguess[-11][10] = 0 | |||||
| Dguess[-11][11] = 0 | |||||
| Dguess[-11][-11] = 0 | |||||
| Dguess[-11][-10] = 0 | |||||
| Dguess[-11][-9] = 2 | |||||
| Dguess[-11][-8] = 0 | |||||
| Dguess[-11][-7] = 0 | |||||
| Dguess[-11][-6] = 0 | |||||
| Dguess[-11][-5] = 0 | |||||
| Dguess[-11][-4] = 0 | |||||
| Dguess[-11][-3] = 0 | |||||
| Dguess[-11][-2] = 0 | |||||
| Dguess[-11][-1] = 11 | |||||
| Dguess[-10] = {} | |||||
| Dguess[-10][0] = 0 | |||||
| Dguess[-10][1] = 0 | |||||
| Dguess[-10][2] = 0 | |||||
| Dguess[-10][3] = 0 | |||||
| Dguess[-10][4] = 0 | |||||
| Dguess[-10][5] = 0 | |||||
| Dguess[-10][6] = 0 | |||||
| Dguess[-10][7] = 0 | |||||
| Dguess[-10][8] = 0 | |||||
| Dguess[-10][9] = 0 | |||||
| Dguess[-10][10] = 0 | |||||
| Dguess[-10][11] = 0 | |||||
| Dguess[-10][-11] = 0 | |||||
| Dguess[-10][-10] = 0 | |||||
| Dguess[-10][-9] = 0 | |||||
| Dguess[-10][-8] = 0 | |||||
| Dguess[-10][-7] = 0 | |||||
| Dguess[-10][-6] = 0 | |||||
| Dguess[-10][-5] = 0 | |||||
| Dguess[-10][-4] = 0 | |||||
| Dguess[-10][-3] = 0 | |||||
| Dguess[-10][-2] = 0 | |||||
| Dguess[-10][-1] = 18 | |||||
| Dguess[-9] = {} | |||||
| Dguess[-9][0] = 0 | |||||
| Dguess[-9][1] = 0 | |||||
| Dguess[-9][2] = 0 | |||||
| Dguess[-9][3] = 0 | |||||
| Dguess[-9][4] = 0 | |||||
| Dguess[-9][5] = 0 | |||||
| Dguess[-9][6] = 0 | |||||
| Dguess[-9][7] = 0 | |||||
| Dguess[-9][8] = 0 | |||||
| Dguess[-9][9] = 0 | |||||
| Dguess[-9][10] = 0 | |||||
| Dguess[-9][11] = 0 | |||||
| Dguess[-9][-11] = 0 | |||||
| Dguess[-9][-10] = 0 | |||||
| Dguess[-9][-9] = 42 | |||||
| Dguess[-9][-8] = 0 | |||||
| Dguess[-9][-7] = 0 | |||||
| Dguess[-9][-6] = 0 | |||||
| Dguess[-9][-5] = 0 | |||||
| Dguess[-9][-4] = 0 | |||||
| Dguess[-9][-3] = 0 | |||||
| Dguess[-9][-2] = 0 | |||||
| Dguess[-9][-1] = 4 | |||||
| Dguess[-8] = {} | |||||
| Dguess[-8][0] = 0 | |||||
| Dguess[-8][1] = 0 | |||||
| Dguess[-8][2] = 0 | |||||
| Dguess[-8][3] = 0 | |||||
| Dguess[-8][4] = 0 | |||||
| Dguess[-8][5] = 0 | |||||
| Dguess[-8][6] = 0 | |||||
| Dguess[-8][7] = 0 | |||||
| Dguess[-8][8] = 0 | |||||
| Dguess[-8][9] = 0 | |||||
| Dguess[-8][10] = 0 | |||||
| Dguess[-8][11] = 0 | |||||
| Dguess[-8][-11] = 0 | |||||
| Dguess[-8][-10] = 0 | |||||
| Dguess[-8][-9] = 0 | |||||
| Dguess[-8][-8] = 107 | |||||
| Dguess[-8][-7] = 0 | |||||
| Dguess[-8][-6] = 0 | |||||
| Dguess[-8][-5] = 0 | |||||
| Dguess[-8][-4] = 0 | |||||
| Dguess[-8][-3] = 0 | |||||
| Dguess[-8][-2] = 0 | |||||
| Dguess[-8][-1] = 0 | |||||
| Dguess[-7] = {} | |||||
| Dguess[-7][0] = 0 | |||||
| Dguess[-7][1] = 0 | |||||
| Dguess[-7][2] = 0 | |||||
| Dguess[-7][3] = 0 | |||||
| Dguess[-7][4] = 0 | |||||
| Dguess[-7][5] = 0 | |||||
| Dguess[-7][6] = 0 | |||||
| Dguess[-7][7] = 0 | |||||
| Dguess[-7][8] = 0 | |||||
| Dguess[-7][9] = 0 | |||||
| Dguess[-7][10] = 0 | |||||
| Dguess[-7][11] = 0 | |||||
| Dguess[-7][-11] = 0 | |||||
| Dguess[-7][-10] = 0 | |||||
| Dguess[-7][-9] = 0 | |||||
| Dguess[-7][-8] = 0 | |||||
| Dguess[-7][-7] = 0 | |||||
| Dguess[-7][-6] = 0 | |||||
| Dguess[-7][-5] = 0 | |||||
| Dguess[-7][-4] = 247 | |||||
| Dguess[-7][-3] = 0 | |||||
| Dguess[-7][-2] = 38 | |||||
| Dguess[-7][-1] = 0 | |||||
| Dguess[-6] = {} | |||||
| Dguess[-6][0] = 0 | |||||
| Dguess[-6][1] = 0 | |||||
| Dguess[-6][2] = 0 | |||||
| Dguess[-6][3] = 0 | |||||
| Dguess[-6][4] = 0 | |||||
| Dguess[-6][5] = 0 | |||||
| Dguess[-6][6] = 0 | |||||
| Dguess[-6][7] = 0 | |||||
| Dguess[-6][8] = 0 | |||||
| Dguess[-6][9] = 0 | |||||
| Dguess[-6][10] = 0 | |||||
| Dguess[-6][11] = 0 | |||||
| Dguess[-6][-11] = 0 | |||||
| Dguess[-6][-10] = 0 | |||||
| Dguess[-6][-9] = 0 | |||||
| Dguess[-6][-8] = 0 | |||||
| Dguess[-6][-7] = 0 | |||||
| Dguess[-6][-6] = 5 | |||||
| Dguess[-6][-5] = 0 | |||||
| Dguess[-6][-4] = 653 | |||||
| Dguess[-6][-3] = 0 | |||||
| Dguess[-6][-2] = 20 | |||||
| Dguess[-6][-1] = 0 | |||||
| Dguess[-5] = {} | |||||
| Dguess[-5][0] = 0 | |||||
| Dguess[-5][1] = 0 | |||||
| Dguess[-5][2] = 0 | |||||
| Dguess[-5][3] = 0 | |||||
| Dguess[-5][4] = 0 | |||||
| Dguess[-5][5] = 0 | |||||
| Dguess[-5][6] = 0 | |||||
| Dguess[-5][7] = 0 | |||||
| Dguess[-5][8] = 0 | |||||
| Dguess[-5][9] = 0 | |||||
| Dguess[-5][10] = 0 | |||||
| Dguess[-5][11] = 0 | |||||
| Dguess[-5][-11] = 0 | |||||
| Dguess[-5][-10] = 0 | |||||
| Dguess[-5][-9] = 0 | |||||
| Dguess[-5][-8] = 0 | |||||
| Dguess[-5][-7] = 0 | |||||
| Dguess[-5][-6] = 0 | |||||
| Dguess[-5][-5] = 259 | |||||
| Dguess[-5][-4] = 0 | |||||
| Dguess[-5][-3] = 316 | |||||
| Dguess[-5][-2] = 9 | |||||
| Dguess[-5][-1] = 836 | |||||
| Dguess[-4] = {} | |||||
| Dguess[-4][0] = 0 | |||||
| Dguess[-4][1] = 0 | |||||
| Dguess[-4][2] = 0 | |||||
| Dguess[-4][3] = 0 | |||||
| Dguess[-4][4] = 0 | |||||
| Dguess[-4][5] = 0 | |||||
| Dguess[-4][6] = 0 | |||||
| Dguess[-4][7] = 0 | |||||
| Dguess[-4][8] = 0 | |||||
| Dguess[-4][9] = 0 | |||||
| Dguess[-4][10] = 0 | |||||
| Dguess[-4][11] = 0 | |||||
| Dguess[-4][-11] = 0 | |||||
| Dguess[-4][-10] = 0 | |||||
| Dguess[-4][-9] = 0 | |||||
| Dguess[-4][-8] = 0 | |||||
| Dguess[-4][-7] = 0 | |||||
| Dguess[-4][-6] = 14 | |||||
| Dguess[-4][-5] = 0 | |||||
| Dguess[-4][-4] = 2523 | |||||
| Dguess[-4][-3] = 0 | |||||
| Dguess[-4][-2] = 99 | |||||
| Dguess[-4][-1] = 0 | |||||
| Dguess[-3] = {} | |||||
| Dguess[-3][0] = 0 | |||||
| Dguess[-3][1] = 0 | |||||
| Dguess[-3][2] = 0 | |||||
| Dguess[-3][3] = 0 | |||||
| Dguess[-3][4] = 0 | |||||
| Dguess[-3][5] = 0 | |||||
| Dguess[-3][6] = 0 | |||||
| Dguess[-3][7] = 0 | |||||
| Dguess[-3][8] = 0 | |||||
| Dguess[-3][9] = 0 | |||||
| Dguess[-3][10] = 0 | |||||
| Dguess[-3][11] = 0 | |||||
| Dguess[-3][-11] = 0 | |||||
| Dguess[-3][-10] = 0 | |||||
| Dguess[-3][-9] = 0 | |||||
| Dguess[-3][-8] = 0 | |||||
| Dguess[-3][-7] = 0 | |||||
| Dguess[-3][-6] = 0 | |||||
| Dguess[-3][-5] = 102 | |||||
| Dguess[-3][-4] = 6 | |||||
| Dguess[-3][-3] = 1744 | |||||
| Dguess[-3][-2] = 2240 | |||||
| Dguess[-3][-1] = 37 | |||||
| Dguess[-2] = {} | |||||
| Dguess[-2][0] = 0 | |||||
| Dguess[-2][1] = 0 | |||||
| Dguess[-2][2] = 0 | |||||
| Dguess[-2][3] = 0 | |||||
| Dguess[-2][4] = 0 | |||||
| Dguess[-2][5] = 0 | |||||
| Dguess[-2][6] = 0 | |||||
| Dguess[-2][7] = 0 | |||||
| Dguess[-2][8] = 0 | |||||
| Dguess[-2][9] = 0 | |||||
| Dguess[-2][10] = 0 | |||||
| Dguess[-2][11] = 0 | |||||
| Dguess[-2][-11] = 0 | |||||
| Dguess[-2][-10] = 0 | |||||
| Dguess[-2][-9] = 0 | |||||
| Dguess[-2][-8] = 0 | |||||
| Dguess[-2][-7] = 0 | |||||
| Dguess[-2][-6] = 0 | |||||
| Dguess[-2][-5] = 40 | |||||
| Dguess[-2][-4] = 24 | |||||
| Dguess[-2][-3] = 1497 | |||||
| Dguess[-2][-2] = 4117 | |||||
| Dguess[-2][-1] = 11 | |||||
| Dguess[-1] = {} | |||||
| Dguess[-1][0] = 0 | |||||
| Dguess[-1][1] = 0 | |||||
| Dguess[-1][2] = 0 | |||||
| Dguess[-1][3] = 0 | |||||
| Dguess[-1][4] = 0 | |||||
| Dguess[-1][5] = 0 | |||||
| Dguess[-1][6] = 0 | |||||
| Dguess[-1][7] = 0 | |||||
| Dguess[-1][8] = 0 | |||||
| Dguess[-1][9] = 0 | |||||
| Dguess[-1][10] = 0 | |||||
| Dguess[-1][11] = 0 | |||||
| Dguess[-1][-11] = 0 | |||||
| Dguess[-1][-10] = 0 | |||||
| Dguess[-1][-9] = 0 | |||||
| Dguess[-1][-8] = 0 | |||||
| Dguess[-1][-7] = 0 | |||||
| Dguess[-1][-6] = 0 | |||||
| Dguess[-1][-5] = 355 | |||||
| Dguess[-1][-4] = 0 | |||||
| Dguess[-1][-3] = 205 | |||||
| Dguess[-1][-2] = 1 | |||||
| Dguess[-1][-1] = 6327 | |||||
| Dguess[-12] = {} | |||||
| Dguess[-12][0] = 0 | |||||
| Dguess[-12][1] = 0 | |||||
| Dguess[-12][2] = 0 | |||||
| Dguess[-12][3] = 0 | |||||
| Dguess[-12][4] = 0 | |||||
| Dguess[-12][5] = 0 | |||||
| Dguess[-12][6] = 0 | |||||
| Dguess[-12][7] = 0 | |||||
| Dguess[-12][8] = 0 | |||||
| Dguess[-12][9] = 0 | |||||
| Dguess[-12][10] = 0 | |||||
| Dguess[-12][11] = 0 | |||||
| Dguess[-12][12] = 0 | |||||
| Dguess[-12][-12] = 1 | |||||
| Dguess[-12][-11] = 0 | |||||
| Dguess[-12][-10] = 0 | |||||
| Dguess[-12][-9] = 0 | |||||
| Dguess[-12][-8] = 0 | |||||
| Dguess[-12][-7] = 0 | |||||
| Dguess[-12][-6] = 0 | |||||
| Dguess[-12][-5] = 0 | |||||
| Dguess[-12][-4] = 0 | |||||
| Dguess[-12][-3] = 0 | |||||
| Dguess[-12][-2] = 0 | |||||
| Dguess[-12][-1] = 0 |
+ 463
- 0
Sec6_applications/Frodo_Single_data/simulation_distribution_NIST2.sage
Прегледај датотеку
| Dguess = {} | |||||
| Dguess[0] = {} | |||||
| Dguess[0][0] = 13205 | |||||
| Dguess[0][1] = 0 | |||||
| Dguess[0][2] = 3 | |||||
| Dguess[0][3] = 0 | |||||
| Dguess[0][4] = 0 | |||||
| Dguess[0][5] = 0 | |||||
| Dguess[0][6] = 0 | |||||
| Dguess[0][7] = 0 | |||||
| Dguess[0][8] = 0 | |||||
| Dguess[0][9] = 0 | |||||
| Dguess[0][10] = 0 | |||||
| Dguess[0][-10] = 0 | |||||
| Dguess[0][-9] = 0 | |||||
| Dguess[0][-8] = 0 | |||||
| Dguess[0][-7] = 0 | |||||
| Dguess[0][-6] = 0 | |||||
| Dguess[0][-5] = 0 | |||||
| Dguess[0][-4] = 0 | |||||
| Dguess[0][-3] = 0 | |||||
| Dguess[0][-2] = 0 | |||||
| Dguess[0][-1] = 0 | |||||
| Dguess[1] = {} | |||||
| Dguess[1][0] = 0 | |||||
| Dguess[1][1] = 10781 | |||||
| Dguess[1][2] = 1396 | |||||
| Dguess[1][3] = 2 | |||||
| Dguess[1][4] = 0 | |||||
| Dguess[1][5] = 0 | |||||
| Dguess[1][6] = 0 | |||||
| Dguess[1][7] = 0 | |||||
| Dguess[1][8] = 0 | |||||
| Dguess[1][9] = 0 | |||||
| Dguess[1][10] = 0 | |||||
| Dguess[1][-10] = 0 | |||||
| Dguess[1][-9] = 0 | |||||
| Dguess[1][-8] = 0 | |||||
| Dguess[1][-7] = 0 | |||||
| Dguess[1][-6] = 0 | |||||
| Dguess[1][-5] = 0 | |||||
| Dguess[1][-4] = 0 | |||||
| Dguess[1][-3] = 0 | |||||
| Dguess[1][-2] = 0 | |||||
| Dguess[1][-1] = 0 | |||||
| Dguess[2] = {} | |||||
| Dguess[2][0] = 0 | |||||
| Dguess[2][1] = 4418 | |||||
| Dguess[2][2] = 4931 | |||||
| Dguess[2][3] = 0 | |||||
| Dguess[2][4] = 0 | |||||
| Dguess[2][5] = 0 | |||||
| Dguess[2][6] = 0 | |||||
| Dguess[2][7] = 0 | |||||
| Dguess[2][8] = 0 | |||||
| Dguess[2][9] = 0 | |||||
| Dguess[2][10] = 0 | |||||
| Dguess[2][-10] = 0 | |||||
| Dguess[2][-9] = 0 | |||||
| Dguess[2][-8] = 0 | |||||
| Dguess[2][-7] = 0 | |||||
| Dguess[2][-6] = 0 | |||||
| Dguess[2][-5] = 0 | |||||
| Dguess[2][-4] = 0 | |||||
| Dguess[2][-3] = 0 | |||||
| Dguess[2][-2] = 0 | |||||
| Dguess[2][-1] = 0 | |||||
| Dguess[3] = {} | |||||
| Dguess[3][0] = 0 | |||||
| Dguess[3][1] = 0 | |||||
| Dguess[3][2] = 0 | |||||
| Dguess[3][3] = 5884 | |||||
| Dguess[3][4] = 0 | |||||
| Dguess[3][5] = 0 | |||||
| Dguess[3][6] = 0 | |||||
| Dguess[3][7] = 0 | |||||
| Dguess[3][8] = 0 | |||||
| Dguess[3][9] = 0 | |||||
| Dguess[3][10] = 0 | |||||
| Dguess[3][-10] = 0 | |||||
| Dguess[3][-9] = 0 | |||||
| Dguess[3][-8] = 0 | |||||
| Dguess[3][-7] = 0 | |||||
| Dguess[3][-6] = 0 | |||||
| Dguess[3][-5] = 0 | |||||
| Dguess[3][-4] = 0 | |||||
| Dguess[3][-3] = 0 | |||||
| Dguess[3][-2] = 0 | |||||
| Dguess[3][-1] = 0 | |||||
| Dguess[4] = {} | |||||
| Dguess[4][0] = 0 | |||||
| Dguess[4][1] = 0 | |||||
| Dguess[4][2] = 0 | |||||
| Dguess[4][3] = 0 | |||||
| Dguess[4][4] = 3038 | |||||
| Dguess[4][5] = 0 | |||||
| Dguess[4][6] = 24 | |||||
| Dguess[4][7] = 0 | |||||
| Dguess[4][8] = 0 | |||||
| Dguess[4][9] = 0 | |||||
| Dguess[4][10] = 0 | |||||
| Dguess[4][-10] = 0 | |||||
| Dguess[4][-9] = 0 | |||||
| Dguess[4][-8] = 0 | |||||
| Dguess[4][-7] = 0 | |||||
| Dguess[4][-6] = 0 | |||||
| Dguess[4][-5] = 0 | |||||
| Dguess[4][-4] = 0 | |||||
| Dguess[4][-3] = 0 | |||||
| Dguess[4][-2] = 0 | |||||
| Dguess[4][-1] = 0 | |||||
| Dguess[5] = {} | |||||
| Dguess[5][0] = 0 | |||||
| Dguess[5][1] = 0 | |||||
| Dguess[5][2] = 0 | |||||
| Dguess[5][3] = 0 | |||||
| Dguess[5][4] = 1 | |||||
| Dguess[5][5] = 1086 | |||||
| Dguess[5][6] = 260 | |||||
| Dguess[5][7] = 2 | |||||
| Dguess[5][8] = 0 | |||||
| Dguess[5][9] = 0 | |||||
| Dguess[5][10] = 0 | |||||
| Dguess[5][-10] = 0 | |||||
| Dguess[5][-9] = 0 | |||||
| Dguess[5][-8] = 0 | |||||
| Dguess[5][-7] = 0 | |||||
| Dguess[5][-6] = 0 | |||||
| Dguess[5][-5] = 0 | |||||
| Dguess[5][-4] = 0 | |||||
| Dguess[5][-3] = 0 | |||||
| Dguess[5][-2] = 0 | |||||
| Dguess[5][-1] = 0 | |||||
| Dguess[6] = {} | |||||
| Dguess[6][0] = 0 | |||||
| Dguess[6][1] = 0 | |||||
| Dguess[6][2] = 0 | |||||
| Dguess[6][3] = 0 | |||||
| Dguess[6][4] = 21 | |||||
| Dguess[6][5] = 235 | |||||
| Dguess[6][6] = 240 | |||||
| Dguess[6][7] = 0 | |||||
| Dguess[6][8] = 0 | |||||
| Dguess[6][9] = 0 | |||||
| Dguess[6][10] = 0 | |||||
| Dguess[6][-10] = 0 | |||||
| Dguess[6][-9] = 0 | |||||
| Dguess[6][-8] = 0 | |||||
| Dguess[6][-7] = 0 | |||||
| Dguess[6][-6] = 0 | |||||
| Dguess[6][-5] = 0 | |||||
| Dguess[6][-4] = 0 | |||||
| Dguess[6][-3] = 0 | |||||
| Dguess[6][-2] = 0 | |||||
| Dguess[6][-1] = 0 | |||||
| Dguess[7] = {} | |||||
| Dguess[7][0] = 0 | |||||
| Dguess[7][1] = 0 | |||||
| Dguess[7][2] = 0 | |||||
| Dguess[7][3] = 0 | |||||
| Dguess[7][4] = 0 | |||||
| Dguess[7][5] = 43 | |||||
| Dguess[7][6] = 0 | |||||
| Dguess[7][7] = 99 | |||||
| Dguess[7][8] = 0 | |||||
| Dguess[7][9] = 0 | |||||
| Dguess[7][10] = 0 | |||||
| Dguess[7][-10] = 0 | |||||
| Dguess[7][-9] = 0 | |||||
| Dguess[7][-8] = 0 | |||||
| Dguess[7][-7] = 0 | |||||
| Dguess[7][-6] = 0 | |||||
| Dguess[7][-5] = 0 | |||||
| Dguess[7][-4] = 0 | |||||
| Dguess[7][-3] = 0 | |||||
| Dguess[7][-2] = 0 | |||||
| Dguess[7][-1] = 0 | |||||
| Dguess[8] = {} | |||||
| Dguess[8][0] = 0 | |||||
| Dguess[8][1] = 4 | |||||
| Dguess[8][2] = 22 | |||||
| Dguess[8][3] = 0 | |||||
| Dguess[8][4] = 0 | |||||
| Dguess[8][5] = 0 | |||||
| Dguess[8][6] = 0 | |||||
| Dguess[8][7] = 0 | |||||
| Dguess[8][8] = 0 | |||||
| Dguess[8][9] = 0 | |||||
| Dguess[8][10] = 0 | |||||
| Dguess[8][-10] = 0 | |||||
| Dguess[8][-9] = 0 | |||||
| Dguess[8][-8] = 0 | |||||
| Dguess[8][-7] = 0 | |||||
| Dguess[8][-6] = 0 | |||||
| Dguess[8][-5] = 0 | |||||
| Dguess[8][-4] = 0 | |||||
| Dguess[8][-3] = 0 | |||||
| Dguess[8][-2] = 0 | |||||
| Dguess[8][-1] = 0 | |||||
| Dguess[9] = {} | |||||
| Dguess[9][0] = 0 | |||||
| Dguess[9][1] = 0 | |||||
| Dguess[9][2] = 0 | |||||
| Dguess[9][3] = 14 | |||||
| Dguess[9][4] = 0 | |||||
| Dguess[9][5] = 0 | |||||
| Dguess[9][6] = 0 | |||||
| Dguess[9][7] = 0 | |||||
| Dguess[9][8] = 0 | |||||
| Dguess[9][9] = 0 | |||||
| Dguess[9][10] = 0 | |||||
| Dguess[9][-10] = 0 | |||||
| Dguess[9][-9] = 0 | |||||
| Dguess[9][-8] = 0 | |||||
| Dguess[9][-7] = 0 | |||||
| Dguess[9][-6] = 0 | |||||
| Dguess[9][-5] = 0 | |||||
| Dguess[9][-4] = 0 | |||||
| Dguess[9][-3] = 0 | |||||
| Dguess[9][-2] = 0 | |||||
| Dguess[9][-1] = 0 | |||||
| Dguess[10] = {} | |||||
| Dguess[10][0] = 0 | |||||
| Dguess[10][1] = 0 | |||||
| Dguess[10][2] = 0 | |||||
| Dguess[10][3] = 10 | |||||
| Dguess[10][4] = 0 | |||||
| Dguess[10][5] = 0 | |||||
| Dguess[10][6] = 0 | |||||
| Dguess[10][7] = 0 | |||||
| Dguess[10][8] = 0 | |||||
| Dguess[10][9] = 0 | |||||
| Dguess[10][10] = 0 | |||||
| Dguess[10][-10] = 0 | |||||
| Dguess[10][-9] = 0 | |||||
| Dguess[10][-8] = 0 | |||||
| Dguess[10][-7] = 0 | |||||
| Dguess[10][-6] = 0 | |||||
| Dguess[10][-5] = 0 | |||||
| Dguess[10][-4] = 0 | |||||
| Dguess[10][-3] = 0 | |||||
| Dguess[10][-2] = 0 | |||||
| Dguess[10][-1] = 0 | |||||
| Dguess[-10] = {} | |||||
| Dguess[-10][0] = 0 | |||||
| Dguess[-10][1] = 0 | |||||
| Dguess[-10][2] = 0 | |||||
| Dguess[-10][3] = 0 | |||||
| Dguess[-10][4] = 0 | |||||
| Dguess[-10][5] = 0 | |||||
| Dguess[-10][6] = 0 | |||||
| Dguess[-10][7] = 0 | |||||
| Dguess[-10][8] = 0 | |||||
| Dguess[-10][9] = 0 | |||||
| Dguess[-10][10] = 0 | |||||
| Dguess[-10][-10] = 0 | |||||
| Dguess[-10][-9] = 0 | |||||
| Dguess[-10][-8] = 0 | |||||
| Dguess[-10][-7] = 0 | |||||
| Dguess[-10][-6] = 0 | |||||
| Dguess[-10][-5] = 0 | |||||
| Dguess[-10][-4] = 0 | |||||
| Dguess[-10][-3] = 0 | |||||
| Dguess[-10][-2] = 0 | |||||
| Dguess[-10][-1] = 10 | |||||
| Dguess[-9] = {} | |||||
| Dguess[-9][0] = 0 | |||||
| Dguess[-9][1] = 0 | |||||
| Dguess[-9][2] = 0 | |||||
| Dguess[-9][3] = 0 | |||||
| Dguess[-9][4] = 0 | |||||
| Dguess[-9][5] = 0 | |||||
| Dguess[-9][6] = 0 | |||||
| Dguess[-9][7] = 0 | |||||
| Dguess[-9][8] = 0 | |||||
| Dguess[-9][9] = 0 | |||||
| Dguess[-9][10] = 0 | |||||
| Dguess[-9][-10] = 0 | |||||
| Dguess[-9][-9] = 12 | |||||
| Dguess[-9][-8] = 0 | |||||
| Dguess[-9][-7] = 0 | |||||
| Dguess[-9][-6] = 0 | |||||
| Dguess[-9][-5] = 0 | |||||
| Dguess[-9][-4] = 0 | |||||
| Dguess[-9][-3] = 0 | |||||
| Dguess[-9][-2] = 0 | |||||
| Dguess[-9][-1] = 2 | |||||
| Dguess[-8] = {} | |||||
| Dguess[-8][0] = 0 | |||||
| Dguess[-8][1] = 0 | |||||
| Dguess[-8][2] = 0 | |||||
| Dguess[-8][3] = 0 | |||||
| Dguess[-8][4] = 0 | |||||
| Dguess[-8][5] = 0 | |||||
| Dguess[-8][6] = 0 | |||||
| Dguess[-8][7] = 0 | |||||
| Dguess[-8][8] = 0 | |||||
| Dguess[-8][9] = 0 | |||||
| Dguess[-8][10] = 0 | |||||
| Dguess[-8][-10] = 0 | |||||
| Dguess[-8][-9] = 0 | |||||
| Dguess[-8][-8] = 43 | |||||
| Dguess[-8][-7] = 0 | |||||
| Dguess[-8][-6] = 0 | |||||
| Dguess[-8][-5] = 0 | |||||
| Dguess[-8][-4] = 0 | |||||
| Dguess[-8][-3] = 0 | |||||
| Dguess[-8][-2] = 0 | |||||
| Dguess[-8][-1] = 0 | |||||
| Dguess[-7] = {} | |||||
| Dguess[-7][0] = 0 | |||||
| Dguess[-7][1] = 0 | |||||
| Dguess[-7][2] = 0 | |||||
| Dguess[-7][3] = 0 | |||||
| Dguess[-7][4] = 0 | |||||
| Dguess[-7][5] = 0 | |||||
| Dguess[-7][6] = 0 | |||||
| Dguess[-7][7] = 0 | |||||
| Dguess[-7][8] = 0 | |||||
| Dguess[-7][9] = 0 | |||||
| Dguess[-7][10] = 0 | |||||
| Dguess[-7][-10] = 0 | |||||
| Dguess[-7][-9] = 0 | |||||
| Dguess[-7][-8] = 0 | |||||
| Dguess[-7][-7] = 0 | |||||
| Dguess[-7][-6] = 0 | |||||
| Dguess[-7][-5] = 0 | |||||
| Dguess[-7][-4] = 100 | |||||
| Dguess[-7][-3] = 0 | |||||
| Dguess[-7][-2] = 0 | |||||
| Dguess[-7][-1] = 0 | |||||
| Dguess[-6] = {} | |||||
| Dguess[-6][0] = 0 | |||||
| Dguess[-6][1] = 0 | |||||
| Dguess[-6][2] = 0 | |||||
| Dguess[-6][3] = 0 | |||||
| Dguess[-6][4] = 0 | |||||
| Dguess[-6][5] = 0 | |||||
| Dguess[-6][6] = 0 | |||||
| Dguess[-6][7] = 0 | |||||
| Dguess[-6][8] = 0 | |||||
| Dguess[-6][9] = 0 | |||||
| Dguess[-6][10] = 0 | |||||
| Dguess[-6][-10] = 0 | |||||
| Dguess[-6][-9] = 0 | |||||
| Dguess[-6][-8] = 0 | |||||
| Dguess[-6][-7] = 0 | |||||
| Dguess[-6][-6] = 0 | |||||
| Dguess[-6][-5] = 0 | |||||
| Dguess[-6][-4] = 462 | |||||
| Dguess[-6][-3] = 0 | |||||
| Dguess[-6][-2] = 1 | |||||
| Dguess[-6][-1] = 0 | |||||
| Dguess[-5] = {} | |||||
| Dguess[-5][0] = 0 | |||||
| Dguess[-5][1] = 0 | |||||
| Dguess[-5][2] = 0 | |||||
| Dguess[-5][3] = 0 | |||||
| Dguess[-5][4] = 0 | |||||
| Dguess[-5][5] = 0 | |||||
| Dguess[-5][6] = 0 | |||||
| Dguess[-5][7] = 0 | |||||
| Dguess[-5][8] = 0 | |||||
| Dguess[-5][9] = 0 | |||||
| Dguess[-5][10] = 0 | |||||
| Dguess[-5][-10] = 0 | |||||
| Dguess[-5][-9] = 0 | |||||
| Dguess[-5][-8] = 0 | |||||
| Dguess[-5][-7] = 0 | |||||
| Dguess[-5][-6] = 0 | |||||
| Dguess[-5][-5] = 619 | |||||
| Dguess[-5][-4] = 0 | |||||
| Dguess[-5][-3] = 0 | |||||
| Dguess[-5][-2] = 371 | |||||
| Dguess[-5][-1] = 236 | |||||
| Dguess[-4] = {} | |||||
| Dguess[-4][0] = 0 | |||||
| Dguess[-4][1] = 0 | |||||
| Dguess[-4][2] = 0 | |||||
| Dguess[-4][3] = 0 | |||||
| Dguess[-4][4] = 0 | |||||
| Dguess[-4][5] = 0 | |||||
| Dguess[-4][6] = 0 | |||||
| Dguess[-4][7] = 0 | |||||
| Dguess[-4][8] = 0 | |||||
| Dguess[-4][9] = 0 | |||||
| Dguess[-4][10] = 0 | |||||
| Dguess[-4][-10] = 0 | |||||
| Dguess[-4][-9] = 0 | |||||
| Dguess[-4][-8] = 0 | |||||
| Dguess[-4][-7] = 0 | |||||
| Dguess[-4][-6] = 2 | |||||
| Dguess[-4][-5] = 0 | |||||
| Dguess[-4][-4] = 3019 | |||||
| Dguess[-4][-3] = 0 | |||||
| Dguess[-4][-2] = 1 | |||||
| Dguess[-4][-1] = 0 | |||||
| Dguess[-3] = {} | |||||
| Dguess[-3][0] = 0 | |||||
| Dguess[-3][1] = 0 | |||||
| Dguess[-3][2] = 0 | |||||
| Dguess[-3][3] = 0 | |||||
| Dguess[-3][4] = 0 | |||||
| Dguess[-3][5] = 0 | |||||
| Dguess[-3][6] = 0 | |||||
| Dguess[-3][7] = 0 | |||||
| Dguess[-3][8] = 0 | |||||
| Dguess[-3][9] = 0 | |||||
| Dguess[-3][10] = 0 | |||||
| Dguess[-3][-10] = 0 | |||||
| Dguess[-3][-9] = 0 | |||||
| Dguess[-3][-8] = 0 | |||||
| Dguess[-3][-7] = 0 | |||||
| Dguess[-3][-6] = 0 | |||||
| Dguess[-3][-5] = 12 | |||||
| Dguess[-3][-4] = 15 | |||||
| Dguess[-3][-3] = 0 | |||||
| Dguess[-3][-2] = 5757 | |||||
| Dguess[-3][-1] = 0 | |||||
| Dguess[-2] = {} | |||||
| Dguess[-2][0] = 0 | |||||
| Dguess[-2][1] = 0 | |||||
| Dguess[-2][2] = 0 | |||||
| Dguess[-2][3] = 0 | |||||
| Dguess[-2][4] = 0 | |||||
| Dguess[-2][5] = 0 | |||||
| Dguess[-2][6] = 0 | |||||
| Dguess[-2][7] = 0 | |||||
| Dguess[-2][8] = 0 | |||||
| Dguess[-2][9] = 0 | |||||
| Dguess[-2][10] = 0 | |||||
| Dguess[-2][-10] = 0 | |||||
| Dguess[-2][-9] = 0 | |||||
| Dguess[-2][-8] = 0 | |||||
| Dguess[-2][-7] = 0 | |||||
| Dguess[-2][-6] = 0 | |||||
| Dguess[-2][-5] = 141 | |||||
| Dguess[-2][-4] = 2 | |||||
| Dguess[-2][-3] = 0 | |||||
| Dguess[-2][-2] = 9126 | |||||
| Dguess[-2][-1] = 3 | |||||
| Dguess[-1] = {} | |||||
| Dguess[-1][0] = 0 | |||||
| Dguess[-1][1] = 0 | |||||
| Dguess[-1][2] = 0 | |||||
| Dguess[-1][3] = 0 | |||||
| Dguess[-1][4] = 0 | |||||
| Dguess[-1][5] = 0 | |||||
| Dguess[-1][6] = 0 | |||||
| Dguess[-1][7] = 0 | |||||
| Dguess[-1][8] = 0 | |||||
| Dguess[-1][9] = 0 | |||||
| Dguess[-1][10] = 0 | |||||
| Dguess[-1][-10] = 0 | |||||
| Dguess[-1][-9] = 0 | |||||
| Dguess[-1][-8] = 0 | |||||
| Dguess[-1][-7] = 0 | |||||
| Dguess[-1][-6] = 0 | |||||
| Dguess[-1][-5] = 867 | |||||
| Dguess[-1][-4] = 0 | |||||
| Dguess[-1][-3] = 0 | |||||
| Dguess[-1][-2] = 33 | |||||
| Dguess[-1][-1] = 11527 |
+ 560
- 0
Sec6_applications/TEST.ipynb
Прегледај датотеку
| { | |||||
| "cells": [ | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 1, | |||||
| "metadata": {}, | |||||
| "outputs": [], | |||||
| "source": [ | |||||
| "load(\"../framework/instance_gen.sage\")" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 2, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "name": "stdout", | |||||
| "output_type": "stream", | |||||
| "text": [ | |||||
| "\u001b[4;37m Build DBDD from LWE \u001b[0m\n", | |||||
| "\u001b[1;33m n= 70 \t m= 70 \t q=3301 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack Estimation \u001b[0m\n", | |||||
| "\u001b[1;33m dim=141 \t δ=1.012362 \t β=45.40 \u001b[0m\n", | |||||
| "\u001b[0m \u001b[0m\n" | |||||
| ] | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "n = 70\n", | |||||
| "m = n\n", | |||||
| "q = 3301\n", | |||||
| "D_s = build_centered_binomial_law(40)\n", | |||||
| "D_e = D_s\n", | |||||
| "A, b, dbdd = initialize_from_LWE_instance(DBDD, n, q, m, D_e, D_s)\n", | |||||
| "# In such parameter range, no need to integrate q-vectors\n", | |||||
| "beta, delta = dbdd.estimate_attack()" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 14, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "name": "stdout", | |||||
| "output_type": "stream", | |||||
| "text": [ | |||||
| "\u001b[4;37m Running the Attack \u001b[0m\n", | |||||
| "1\n" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "ename": "ValueError", | |||||
| "evalue": "Float type 'ld' not understood.", | |||||
| "output_type": "error", | |||||
| "traceback": [ | |||||
| "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m", | |||||
| "\u001b[0;31mValueError\u001b[0m Traceback (most recent call last)", | |||||
| "\u001b[0;32m<ipython-input-14-b4e7e86f62fe>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0msecret\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mdbdd\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mattack\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m", | |||||
| "\u001b[0;32m<string>\u001b[0m in \u001b[0;36mattack\u001b[0;34m(self, beta_max, beta_pre, randomize, tours)\u001b[0m\n", | |||||
| "\u001b[0;32msrc/fpylll/fplll/gso.pyx\u001b[0m in \u001b[0;36mfpylll.fplll.gso.MatGSO.__init__\u001b[0;34m()\u001b[0m\n", | |||||
| "\u001b[0;31mValueError\u001b[0m: Float type 'ld' not understood." | |||||
| ] | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "secret = dbdd.attack()" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 3, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "data": { | |||||
| "text/plain": [ | |||||
| "(17, -12, 9, -15)" | |||||
| ] | |||||
| }, | |||||
| "execution_count": 3, | |||||
| "metadata": {}, | |||||
| "output_type": "execute_result" | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "# Simulating perfect hints\n", | |||||
| "v0 = vec([randint(0, 1) for i in range(m + n)])\n", | |||||
| "v1 = vec([randint(0, 1) for i in range(m + n)])\n", | |||||
| "v2 = vec([randint(0, 1) for i in range(m + n)])\n", | |||||
| "v3 = vec([randint(0, 1) for i in range(m + n)]) \n", | |||||
| "# Computing l = <vi, s>\n", | |||||
| "dbdd.leak(v0), dbdd.leak(v1), dbdd.leak(v2), dbdd.leak(v3)" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 4, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "name": "stdout", | |||||
| "output_type": "stream", | |||||
| "text": [ | |||||
| "\u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=140, δ=1.01252495, β=41.94 \u001b[0m\n", | |||||
| "\u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=139, δ=1.01275154, β=38.44 \u001b[0m\n", | |||||
| "\u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=138, δ=1.01293762, β=34.79 \u001b[0m\n", | |||||
| "\u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=137, δ=1.01314871, β=30.92 \u001b[0m\n" | |||||
| ] | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "_ = dbdd.integrate_perfect_hint(v0, 25) \n", | |||||
| "_ = dbdd.integrate_perfect_hint(v1, 12) \n", | |||||
| "_ = dbdd.integrate_perfect_hint(v2, -14) \n", | |||||
| "_ = dbdd.integrate_perfect_hint(v3, -3)" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 5, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "data": { | |||||
| "text/plain": [ | |||||
| "(1, 1, 0, 3)" | |||||
| ] | |||||
| }, | |||||
| "execution_count": 5, | |||||
| "metadata": {}, | |||||
| "output_type": "execute_result" | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "# Simulating modular hints\n", | |||||
| "v0 = vec([randint(0, 1) for i in range(m + n)])\n", | |||||
| "v1 = vec([randint(0, 1) for i in range(m + n)])\n", | |||||
| "v2 = vec([randint(0, 1) for i in range(m + n)])\n", | |||||
| "v3 = vec([randint(0, 1) for i in range(m + n)]) \n", | |||||
| "# Computing l = <vi, s> mod k\n", | |||||
| "dbdd.leak(v0)%2, dbdd.leak(v1)%3, dbdd.leak(v2)%4, dbdd.leak(v3)%5" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 6, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "name": "stdout", | |||||
| "output_type": "stream", | |||||
| "text": [ | |||||
| "\u001b[1;37m integrate modular hint \u001b[0m \u001b[0m (smooth) \u001b[0m " | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "ename": "NotImplementedError", | |||||
| "evalue": "", | |||||
| "output_type": "error", | |||||
| "traceback": [ | |||||
| "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m", | |||||
| "\u001b[0;31mNotImplementedError\u001b[0m Traceback (most recent call last)", | |||||
| "\u001b[0;32m<ipython-input-6-0bba940b5cde>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0;31m# Integrate modular hints\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 2\u001b[0;31m \u001b[0m_\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mdbdd\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrate_modular_hint\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mv0\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mInteger\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mInteger\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m2\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;32mFalse\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m\u001b[1;32m 3\u001b[0m \u001b[0m_\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mdbdd\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrate_modular_hint\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mv1\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mInteger\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m1\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mInteger\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m3\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 4\u001b[0m \u001b[0m_\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mdbdd\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrate_modular_hint\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mv2\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mInteger\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m0\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mInteger\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m4\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[1;32m 5\u001b[0m \u001b[0m_\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mdbdd\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mintegrate_modular_hint\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mv3\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mInteger\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m3\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mInteger\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m5\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0;32mTrue\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n", | |||||
| "\u001b[0;32m<string>\u001b[0m in \u001b[0;36mdecorated\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n", | |||||
| "\u001b[0;32m<string>\u001b[0m in \u001b[0;36mdecorated\u001b[0;34m(self, *args, **kwargs)\u001b[0m\n", | |||||
| "\u001b[0;32m<string>\u001b[0m in \u001b[0;36mintegrate_modular_hint\u001b[0;34m(self, v, l, k, smooth)\u001b[0m\n", | |||||
| "\u001b[0;31mNotImplementedError\u001b[0m: " | |||||
| ] | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "# Integrate modular hints\n", | |||||
| "_ = dbdd.integrate_modular_hint(v0, 1, 2, False) \n", | |||||
| "_ = dbdd.integrate_modular_hint(v1, 1, 3, True)\n", | |||||
| "_ = dbdd.integrate_modular_hint(v2, 0, 4, True) \n", | |||||
| "_ = dbdd.integrate_modular_hint(v3, 3, 5, True)" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 19, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "data": { | |||||
| "text/plain": [ | |||||
| "(-5, 24, 9, 54)" | |||||
| ] | |||||
| }, | |||||
| "execution_count": 19, | |||||
| "metadata": {}, | |||||
| "output_type": "execute_result" | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "# Simulating approximate hints\n", | |||||
| "v0 = vec([randint(0, 1) for i in range(m + n)])\n", | |||||
| "v1 = vec([randint(0, 1) for i in range(m + n)])\n", | |||||
| "v2 = vec([randint(0, 1) for i in range(m + n)])\n", | |||||
| "v3 = vec([randint(0, 1) for i in range(m + n)]) \n", | |||||
| "# Computing l = <vi, s> + noise\n", | |||||
| "dbdd.leak(v0) + 2, dbdd.leak(v1) + 1, dbdd.leak(v2) - 1, dbdd.leak(v3)" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 20, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "name": "stdout", | |||||
| "output_type": "stream", | |||||
| "text": [ | |||||
| "\u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (conditionning) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=137, δ=1.01334785, β=26.99 \u001b[0m\n", | |||||
| "\u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (conditionning) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=137, δ=1.01342129, β=25.49 \u001b[0m\n", | |||||
| "\u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (conditionning) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=137, δ=1.01350341, β=24.44 \u001b[0m\n", | |||||
| "\u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (conditionning) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=137, δ=1.01362755, β=23.65 \u001b[0m\n" | |||||
| ] | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "# Integrate approximate hints\n", | |||||
| "var = 10\n", | |||||
| "_ = dbdd.integrate_approx_hint(v0, -5, var, aposteriori=False) \n", | |||||
| "_ = dbdd.integrate_approx_hint(v1, 24, var, aposteriori=False) \n", | |||||
| "_ = dbdd.integrate_approx_hint(v2, 9, var, aposteriori=False) \n", | |||||
| "_ = dbdd.integrate_approx_hint(v3, 54, var, aposteriori=False)" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 21, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "name": "stdout", | |||||
| "output_type": "stream", | |||||
| "text": [ | |||||
| "\u001b[4;37m Attack Estimation \u001b[0m\n", | |||||
| "\u001b[1;33m dim=137 \t δ=1.013628 \t β=23.65 \u001b[0m\n", | |||||
| "\u001b[0m \u001b[0m\n", | |||||
| "\u001b[4;37m Running the Attack \u001b[0m\n", | |||||
| "1\n" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "ename": "ValueError", | |||||
| "evalue": "Float type 'ld' not understood.", | |||||
| "output_type": "error", | |||||
| "traceback": [ | |||||
| "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m", | |||||
| "\u001b[0;31mValueError\u001b[0m Traceback (most recent call last)", | |||||
| "\u001b[0;32m<ipython-input-21-7c2ddea6b769>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0mbeta\u001b[0m\u001b[0;34m,\u001b[0m \u001b[0mdelta\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mdbdd\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mestimate_attack\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 2\u001b[0;31m \u001b[0msecret\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0mdbdd\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mattack\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m", | |||||
| "\u001b[0;32m<string>\u001b[0m in \u001b[0;36mattack\u001b[0;34m(self, beta_max, beta_pre, randomize, tours)\u001b[0m\n", | |||||
| "\u001b[0;32msrc/fpylll/fplll/gso.pyx\u001b[0m in \u001b[0;36mfpylll.fplll.gso.MatGSO.__init__\u001b[0;34m()\u001b[0m\n", | |||||
| "\u001b[0;31mValueError\u001b[0m: Float type 'ld' not understood." | |||||
| ] | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "beta, delta = dbdd.estimate_attack()\n", | |||||
| "secret = dbdd.attack()" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 23, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "name": "stdout", | |||||
| "output_type": "stream", | |||||
| "text": [ | |||||
| "\u001b[0m --- Demonstration mode (no averaging) --- \u001b[0m\n", | |||||
| "\u001b[0m Set of parameters: CCS1 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack without hints: 268.83 bikz \u001b[0m\n", | |||||
| "\u001b[4;37m Build DBDD from LWE \u001b[0m\n", | |||||
| "\u001b[1;33m n=352 \t m=352 \t q=2048 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u0 = -1.047495308214138 + χ(σ²=0.074) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=705, δ=1.00520912, β=268.64 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u50 = 1.211598111935266 + χ(σ²=0.177) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=705, δ=1.00533686, β=258.80 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u100 = -1.047495308214138 + χ(σ²=0.074) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=705, δ=1.00547581, β=248.73 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u150 = 1.211598111935266 + χ(σ²=0.177) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=705, δ=1.00560729, β=239.71 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u200 = 0.00843621399176955 + χ(σ²=0.016) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=705, δ=1.00573966, β=231.20 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u250 = 1.211598111935266 + χ(σ²=0.177) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=705, δ=1.00587017, β=223.15 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u300 = 0.00843621399176955 + χ(σ²=0.016) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=705, δ=1.00600691, β=214.98 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u350 = 0.00843621399176955 + χ(σ²=0.016) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=705, δ=1.00613813, β=207.71 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u351 = 1.211598111935266 + χ(σ²=0.177) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=705, δ=1.00614016, β=207.61 \u001b[0m\n", | |||||
| "\u001b[4;37m Integrating q-vectors \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 2048*c703 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=704, δ=1.00614274, β=207.50 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 2048*c653 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=654, δ=1.00623802, β=202.43 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 2048*c603 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=604, δ=1.00629226, β=199.59 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack Estimation \u001b[0m\n", | |||||
| "\u001b[3;34m ln(dvol)=2229.2964391 \t ln(Bvol)=1761.2869858 \t ln(Svol)=-936.0189067 \tδ(β)=100000000000000000000.000000 \u001b[0m\n", | |||||
| "\u001b[1;33m dim=584 \t δ=1.006299 \t β=199.30 \u001b[0m\n", | |||||
| "\u001b[0m \u001b[0m\n", | |||||
| "\u001b[4;37m Hybrid attack estimation \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=517 \t delta=1.007041 \t beta=165.65 \t guesses= 50 \u001b[0m \u001b[1;33m Proba success = 0.784776775862473 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=449 \t delta=1.008001 \t beta=132.43 \t guesses= 100 \u001b[0m \u001b[1;33m Proba success = 0.615874587933098 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=374 \t delta=1.009401 \t beta=96.94 \t guesses= 150 \u001b[0m \u001b[1;33m Proba success = 0.227714429544019 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=295 \t delta=1.011563 \t beta=58.46 \t guesses= 200 \u001b[0m \u001b[1;33m Proba success = 0.0417737457149379 \u001b[0m\n", | |||||
| "\u001b[0m Set of parameters: CCS2 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack without hints: 447.85 bikz \u001b[0m\n", | |||||
| "\u001b[4;37m Build DBDD from LWE \u001b[0m\n", | |||||
| "\u001b[1;33m n=592 \t m=592 \t q=4096 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u0 = 0.000494369678659709 + χ(σ²=0.001) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00368084, β=447.74 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u50 = 1.146460874616214 + χ(σ²=0.127) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00376168, β=434.18 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u100 = 0.000494369678659709 + χ(σ²=0.001) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00383428, β=422.44 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u150 = -1.00569376313933 + χ(σ²=0.011) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00391176, β=410.48 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u200 = -1.00569376313933 + χ(σ²=0.011) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00398557, β=399.57 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u250 = 0.000494369678659709 + χ(σ²=0.001) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00406105, β=388.84 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u300 = -1.00569376313933 + χ(σ²=0.011) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00412447, β=380.28 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u350 = 0.000494369678659709 + χ(σ²=0.001) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00419601, β=370.82 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u400 = -1.00569376313933 + χ(σ²=0.011) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00426402, β=362.29 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u450 = -1.00569376313933 + χ(σ²=0.011) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00433281, β=353.83 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u500 = 1.146460874616214 + χ(σ²=0.127) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00440385, β=345.52 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u550 = -1.00569376313933 + χ(σ²=0.011) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00447868, β=337.11 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u591 = 0.000494369678659709 + χ(σ²=0.001) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1185, δ=1.00453370, β=331.08 \u001b[0m\n", | |||||
| "\u001b[4;37m Integrating q-vectors \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 4096*c1183 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1184, δ=1.00453416, β=330.92 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 4096*c1133 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1134, δ=1.00460786, β=323.20 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 4096*c1083 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1084, δ=1.00467681, β=316.15 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 4096*c1033 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1034, δ=1.00473859, β=309.91 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 4096*c983 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=984, δ=1.00479311, β=304.69 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 4096*c933 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=934, δ=1.00483487, β=300.74 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 4096*c883 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=884, δ=1.00485996, β=298.46 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack Estimation \u001b[0m\n", | |||||
| "\u001b[3;34m ln(dvol)=3529.6911796 \t ln(Bvol)=2195.8902680 \t ln(Svol)=-2667.6018232 \tδ(β)=100000000000000000000.000000 \u001b[0m\n", | |||||
| "\u001b[1;33m dim=857 \t δ=1.004864 \t β=298.11 \u001b[0m\n", | |||||
| "\u001b[0m \u001b[0m\n", | |||||
| "\u001b[4;37m Hybrid attack estimation \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=804 \t delta=1.005161 \t beta=272.46 \t guesses= 50 \u001b[0m \u001b[1;33m Proba success = 0.986359509012097 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=750 \t delta=1.005502 \t beta=247.03 \t guesses= 100 \u001b[0m \u001b[1;33m Proba success = 0.972905081018585 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=696 \t delta=1.005890 \t beta=221.82 \t guesses= 150 \u001b[0m \u001b[1;33m Proba success = 0.959634178028866 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=642 \t delta=1.006345 \t beta=196.85 \t guesses= 200 \u001b[0m \u001b[1;33m Proba success = 0.946544296671780 \u001b[0m\n", | |||||
| "\u001b[0m Set of parameters: CCS3 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack without hints: 491.98 bikz \u001b[0m\n" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "name": "stdout", | |||||
| "output_type": "stream", | |||||
| "text": [ | |||||
| "\u001b[4;37m Build DBDD from LWE \u001b[0m\n", | |||||
| "\u001b[1;33m n=752 \t m=752 \t q=32768 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u0 = -2.187046263345110 + χ(σ²=0.163) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1505, δ=1.00344395, β=491.89 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u50 = 1.201824086229531 + χ(σ²=0.162) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1505, δ=1.00349544, β=481.73 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u100 = -1.01352265043897 + χ(σ²=0.030) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00354986, β=471.38 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u150 = -1.01352265043897 + χ(σ²=0.030) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00359717, β=462.61 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u200 = 0.0001125935934245342 + χ(σ²=0.000) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00363783, β=455.33 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u250 = -1.01352265043897 + χ(σ²=0.030) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00369078, β=445.99 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u300 = 1.604094165813716 + χ(σ²=0.242) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00373686, β=438.27 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u350 = 1.201824086229531 + χ(σ²=0.162) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00378107, β=430.89 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u400 = 1.201824086229531 + χ(σ²=0.162) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00382418, β=424.06 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u450 = 1.201824086229531 + χ(σ²=0.162) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00386791, β=417.19 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u500 = 1.201824086229531 + χ(σ²=0.162) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00392265, β=408.79 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u550 = 0.0001125935934245342 + χ(σ²=0.000) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00396794, β=402.16 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u600 = -1.01352265043897 + χ(σ²=0.030) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00401167, β=395.78 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u650 = 2.998692810457516 + χ(σ²=0.003) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1504, δ=1.00406457, β=388.40 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u700 = 0.0001125935934245342 + χ(σ²=0.000) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1503, δ=1.00411096, β=382.00 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u750 = 0.0001125935934245342 + χ(σ²=0.000) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1503, δ=1.00416366, β=374.99 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u751 = -1.01352265043897 + χ(σ²=0.030) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1503, δ=1.00416457, β=374.89 \u001b[0m\n", | |||||
| "\u001b[4;37m Integrating q-vectors \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1503 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1502, δ=1.00416557, β=374.77 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1453 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1452, δ=1.00420958, β=369.15 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1403 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1402, δ=1.00424963, β=364.09 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1353 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1352, δ=1.00428447, β=359.71 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1303 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1302, δ=1.00431461, β=356.11 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1253 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1252, δ=1.00433620, β=353.47 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1203 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1202, δ=1.00434902, β=352.01 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack Estimation \u001b[0m\n", | |||||
| "\u001b[3;34m ln(dvol)=5873.7705379 \t ln(Bvol)=4429.2104838 \t ln(Svol)=-2889.1201083 \tδ(β)=100000000000000000000.000000 \u001b[0m\n", | |||||
| "\u001b[1;33m dim=1177 \t δ=1.004350 \t β=351.81 \u001b[0m\n", | |||||
| "\u001b[0m \u001b[0m\n", | |||||
| "\u001b[4;37m Hybrid attack estimation \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=1122 \t delta=1.004547 \t beta=329.58 \t guesses= 50 \u001b[0m \u001b[1;33m Proba success = 0.997189039098024 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=1068 \t delta=1.004764 \t beta=307.51 \t guesses= 100 \u001b[0m \u001b[1;33m Proba success = 0.994385979697240 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=1013 \t delta=1.005004 \t beta=285.60 \t guesses= 150 \u001b[0m \u001b[1;33m Proba success = 0.991590799586837 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=959 \t delta=1.005270 \t beta=263.86 \t guesses= 200 \u001b[0m \u001b[1;33m Proba success = 0.988803476618439 \u001b[0m\n", | |||||
| "\u001b[0m Set of parameters: CCS4 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack without hints: 584.09 bikz \u001b[0m\n", | |||||
| "\u001b[4;37m Build DBDD from LWE \u001b[0m\n", | |||||
| "\u001b[1;33m n=864 \t m=864 \t q=32768 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u0 = 3.00000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1728, δ=1.00304787, β=583.29 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u50 = 0.000000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1712, δ=1.00311466, β=566.08 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u100 = 4.03571428571429 + χ(σ²=0.066) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1698, δ=1.00317667, β=550.73 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u150 = 0.000000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1686, δ=1.00323493, β=536.95 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u200 = 0.000000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1671, δ=1.00330361, β=521.49 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u250 = 1.635097971811619 + χ(σ²=0.234) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1649, δ=1.00339599, β=501.70 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u300 = -1.009176115880109 + χ(σ²=0.026) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1632, δ=1.00347647, β=485.47 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u350 = -1.009176115880109 + χ(σ²=0.026) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1613, δ=1.00356554, β=468.44 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u400 = 1.190473351615596 + χ(σ²=0.156) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1602, δ=1.00362960, β=456.74 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u450 = 1.190473351615596 + χ(σ²=0.156) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1585, δ=1.00371670, β=441.61 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u500 = 3.00000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1567, δ=1.00381197, β=425.91 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u550 = 1.190473351615596 + χ(σ²=0.156) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1554, δ=1.00389208, β=413.45 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u600 = 0.000000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1535, δ=1.00399725, β=397.84 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u650 = 0.000000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1518, δ=1.00409770, β=383.81 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u700 = -1.009176115880109 + χ(σ²=0.026) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1503, δ=1.00419478, β=371.06 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u750 = 1.190473351615596 + χ(σ²=0.156) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1490, δ=1.00428223, β=359.95 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u800 = -1.009176115880109 + χ(σ²=0.026) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1475, δ=1.00438267, β=347.93 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u850 = 1.635097971811619 + χ(σ²=0.234) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1459, δ=1.00449591, β=335.17 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u863 = 0.000000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1455, δ=1.00452419, β=332.09 \u001b[0m\n", | |||||
| "\u001b[4;37m Integrating q-vectors \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1727 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1454, δ=1.00452460, β=331.95 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1677 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1404, δ=1.00458760, β=325.29 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1627 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1354, δ=1.00464808, β=319.05 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1577 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1304, δ=1.00470490, β=313.30 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1527 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1254, δ=1.00475783, β=308.13 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1477 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1204, δ=1.00480390, β=303.65 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1427 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1154, δ=1.00484348, β=300.02 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1377 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1104, δ=1.00487098, β=297.43 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1327 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1054, δ=1.00488544, β=296.15 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack Estimation \u001b[0m\n", | |||||
| "\u001b[3;34m ln(dvol)=5223.8138965 \t ln(Bvol)=4657.9490534 \t ln(Svol)=-1131.7296863 \tδ(β)=100000000000000000000.000000 \u001b[0m\n", | |||||
| "\u001b[1;33m dim=1039 \t δ=1.004886 \t β=296.07 \u001b[0m\n", | |||||
| "\u001b[0m \u001b[0m\n", | |||||
| "\u001b[4;37m Hybrid attack estimation \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=963 \t delta=1.005249 \t beta=265.50 \t guesses= 50 \u001b[0m \u001b[1;33m Proba success = 0.818477853233848 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=886 \t delta=1.005675 \t beta=235.28 \t guesses= 100 \u001b[0m \u001b[1;33m Proba success = 0.669905996234288 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=808 \t delta=1.006181 \t beta=205.45 \t guesses= 150 \u001b[0m \u001b[1;33m Proba success = 0.548303221666322 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=729 \t delta=1.006800 \t beta=175.62 \t guesses= 200 \u001b[0m \u001b[1;33m Proba success = 0.256443378603881 \u001b[0m\n", | |||||
| "\u001b[0m Set of parameters: NIST1 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack without hints: 487.00 bikz \u001b[0m\n", | |||||
| "\u001b[4;37m Build DBDD from LWE \u001b[0m\n", | |||||
| "\u001b[1;33m n=640 \t m=640 \t q=32768 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u0 = 3.069447793585725 + χ(σ²=0.444) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1281, δ=1.00346927, β=486.85 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u50 = 1.321045392022008 + χ(σ²=0.399) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1271, δ=1.00354851, β=471.62 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u100 = 1.755049101352603 + χ(σ²=0.765) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1266, δ=1.00360481, β=461.28 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u150 = -4.57717926440819 + χ(σ²=1.097) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1262, δ=1.00365626, β=451.99 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u200 = 4.090359168241965 + χ(σ²=0.159) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1253, δ=1.00373273, β=438.88 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u250 = -2.41906805640610 + χ(σ²=0.436) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1243, δ=1.00381626, β=425.31 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u300 = -2.661084529507207 + χ(σ²=0.837) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1235, δ=1.00389158, β=413.53 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u350 = -2.41906805640610 + χ(σ²=0.436) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1230, δ=1.00395482, β=404.11 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u400 = 1.321045392022008 + χ(σ²=0.399) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1223, δ=1.00403038, β=393.22 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u450 = -2.661084529507207 + χ(σ²=0.837) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1216, δ=1.00410464, β=382.87 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u500 = 1.321045392022008 + χ(σ²=0.399) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1211, δ=1.00417085, β=374.17 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u550 = 4.090359168241965 + χ(σ²=0.159) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1206, δ=1.00423643, β=365.69 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u600 = 1.755049101352603 + χ(σ²=0.765) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1194, δ=1.00434773, β=352.15 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u639 = -1.515323025952966 + χ(σ²=1.992) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1189, δ=1.00441030, β=344.75 \u001b[0m\n", | |||||
| "\u001b[4;37m Integrating q-vectors \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1279 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1188, δ=1.00441100, β=344.68 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1229 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1138, δ=1.00443703, β=341.70 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 32768*c1179 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1088, δ=1.00445220, β=340.08 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack Estimation \u001b[0m\n", | |||||
| "\u001b[3;34m ln(dvol)=4931.2206559 \t ln(Bvol)=5364.9591775 \t ln(Svol)=867.4770433 \tδ(β)=100000000000000000000.000000 \u001b[0m\n", | |||||
| "\u001b[1;33m dim=1065 \t δ=1.004453 \t β=339.89 \u001b[0m\n", | |||||
| "\u001b[0m \u001b[0m\n", | |||||
| "\u001b[4;37m Hybrid attack estimation \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=978 \t delta=1.004823 \t beta=301.82 \t guesses= 50 \u001b[0m \u001b[1;33m Proba success = 0.333906700218510 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=884 \t delta=1.005297 \t beta=261.80 \t guesses= 100 \u001b[0m \u001b[1;33m Proba success = 0.00102495772223270 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=787 \t delta=1.005904 \t beta=221.11 \t guesses= 150 \u001b[0m \u001b[1;33m Proba success = 1.17943929438748e-6 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=691 \t delta=1.006660 \t beta=181.81 \t guesses= 200 \u001b[0m \u001b[1;33m Proba success = 7.67683727015403e-12 \u001b[0m\n", | |||||
| "\u001b[0m Set of parameters: NIST2 \u001b[0m\n", | |||||
| "\u001b[4;37m Attack without hints: 708.06 bikz \u001b[0m\n", | |||||
| "\u001b[4;37m Build DBDD from LWE \u001b[0m\n", | |||||
| "\u001b[1;33m n=976 \t m=976 \t q=65536 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u0 = 1.292442281128725 + χ(σ²=0.218) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1953, δ=1.00264550, β=707.92 \u001b[0m\n" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "name": "stdout", | |||||
| "output_type": "stream", | |||||
| "text": [ | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u50 = 3.025380710659899 + χ(σ²=0.169) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1950, δ=1.00267055, β=699.04 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u100 = -2.447576689126436 + χ(σ²=0.398) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1942, δ=1.00270492, β=686.89 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u150 = 5.235337243401759 + χ(σ²=0.243) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1932, δ=1.00274506, β=673.32 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u200 = 1.292442281128725 + χ(σ²=0.218) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1923, δ=1.00278259, β=660.89 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u250 = 4.01405228758170 + χ(σ²=0.028) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1917, δ=1.00281478, β=650.62 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u300 = 3.025380710659899 + χ(σ²=0.169) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1907, δ=1.00285614, β=637.75 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u350 = 0.000000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1895, δ=1.00290400, β=623.42 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u400 = 0.000000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1884, δ=1.00295046, β=610.02 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u450 = -2.447576689126436 + χ(σ²=0.398) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1875, δ=1.00299260, β=598.21 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u500 = 0.000000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1862, δ=1.00304489, β=583.99 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u550 = -2.447576689126436 + χ(σ²=0.398) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1851, δ=1.00309357, β=571.39 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u600 = 1.292442281128725 + χ(σ²=0.218) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1845, δ=1.00312943, β=562.34 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u650 = 3.025380710659899 + χ(σ²=0.169) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1840, δ=1.00316311, β=553.98 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u700 = 4.01405228758170 + χ(σ²=0.028) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1832, δ=1.00320516, β=543.91 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u750 = 1.292442281128725 + χ(σ²=0.218) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1824, δ=1.00324807, β=533.92 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate perfect hint \u001b[0m \u001b[3;34m u800 = 0.000000000000000 \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1814, δ=1.00329760, β=522.78 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u850 = -1.089403973506705 + χ(σ²=0.393) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1808, δ=1.00333637, β=514.35 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u900 = -2.447576689126436 + χ(σ²=0.398) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1801, δ=1.00337834, β=505.41 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u950 = 4.01405228758170 + χ(σ²=0.028) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1792, δ=1.00342669, β=495.42 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate approx hint \u001b[0m \u001b[0m (aposteriori) \u001b[0m \u001b[3;34m u975 = 1.292442281128725 + χ(σ²=0.218) \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1789, δ=1.00344645, β=491.43 \u001b[0m\n", | |||||
| "\u001b[4;37m Integrating q-vectors \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 65536*c1951 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1788, δ=1.00344701, β=491.33 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 65536*c1901 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1738, δ=1.00347079, β=486.57 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 65536*c1851 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1688, δ=1.00349212, β=482.41 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 65536*c1801 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1638, δ=1.00350973, β=478.94 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 65536*c1751 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1588, δ=1.00352409, β=476.27 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 65536*c1701 ∈ Λ \u001b[0m \u001b[3;32m \t Worthy hint ! \u001b[0m \u001b[1;33m dim=1538, δ=1.00353300, β=474.54 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;37m integrate short vector hint \u001b[0m \u001b[3;34m 65536*c1651 ∈ Λ \u001b[0m \u001b[3;31m \t Unworthy hint, Rejected. \u001b[0m\n", | |||||
| "\u001b[4;37m Attack Estimation \u001b[0m\n", | |||||
| "\u001b[3;34m ln(dvol)=7436.1356246 \t ln(Bvol)=7497.0799049 \t ln(Svol)=121.8885608 \tδ(β)=100000000000000000000.000000 \u001b[0m\n", | |||||
| "\u001b[1;33m dim=1489 \t δ=1.003536 \t β=473.94 \u001b[0m\n", | |||||
| "\u001b[0m \u001b[0m\n", | |||||
| "\u001b[4;37m Hybrid attack estimation \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=1405 \t delta=1.003735 \t beta=438.59 \t guesses= 50 \u001b[0m \u001b[1;33m Proba success = 0.802156595500351 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=1324 \t delta=1.003948 \t beta=405.08 \t guesses= 100 \u001b[0m \u001b[1;33m Proba success = 0.603232864940319 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=1240 \t delta=1.004199 \t beta=370.52 \t guesses= 150 \u001b[0m \u001b[1;33m Proba success = 0.265895477646676 \u001b[0m\n", | |||||
| "\u001b[0m [...50] \u001b[0m \u001b[1;33m dim=1152 \t delta=1.004501 \t beta=334.55 \t guesses= 200 \u001b[0m \u001b[1;33m Proba success = 0.0905624388817529 \u001b[0m\n" | |||||
| ] | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "load('exploiting_SCA_from_Bos_et_al.sage')" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": 25, | |||||
| "metadata": {}, | |||||
| "outputs": [ | |||||
| { | |||||
| "ename": "TypeError", | |||||
| "evalue": "version() takes 0 positional arguments but 1 was given", | |||||
| "output_type": "error", | |||||
| "traceback": [ | |||||
| "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m", | |||||
| "\u001b[0;31mTypeError\u001b[0m Traceback (most recent call last)", | |||||
| "\u001b[0;32m<ipython-input-25-576b6e31d0fc>\u001b[0m in \u001b[0;36m<module>\u001b[0;34m()\u001b[0m\n\u001b[1;32m 1\u001b[0m \u001b[0;32mimport\u001b[0m \u001b[0mfpylll\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0;32m----> 2\u001b[0;31m \u001b[0mversion\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0mfpylll\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m", | |||||
| "\u001b[0;31mTypeError\u001b[0m: version() takes 0 positional arguments but 1 was given" | |||||
| ] | |||||
| } | |||||
| ], | |||||
| "source": [ | |||||
| "import fpylll\n", | |||||
| "version(fpylll)" | |||||
| ] | |||||
| }, | |||||
| { | |||||
| "cell_type": "code", | |||||
| "execution_count": null, | |||||
| "metadata": {}, | |||||
| "outputs": [], | |||||
| "source": [] | |||||
| } | |||||
| ], | |||||
| "metadata": { | |||||
| "kernelspec": { | |||||
| "display_name": "SageMath 9.0", | |||||
| "language": "sage", | |||||
| "name": "sagemath" | |||||
| }, | |||||
| "language_info": { | |||||
| "codemirror_mode": { | |||||
| "name": "ipython", | |||||
| "version": 3 | |||||
| }, | |||||
| "file_extension": ".py", | |||||
| "mimetype": "text/x-python", | |||||
| "name": "python", | |||||
| "nbconvert_exporter": "python", | |||||
| "pygments_lexer": "ipython3", | |||||
| "version": "3.7.3" | |||||
| } | |||||
| }, | |||||
| "nbformat": 4, | |||||
| "nbformat_minor": 2 | |||||
| } |
+ 196
- 0
Sec6_applications/exploiting_SCA_attack.sage
Прегледај датотеку
| #!/usr/bin/sage -python | |||||
| # -*- coding: latin-1 -*- | |||||
| load("../framework/instance_gen.sage") | |||||
| for params in ['CCS1']: | |||||
| logging("Set of parameters: " + params) | |||||
| if params == 'challenge': | |||||
| n = 296 | |||||
| m = n + 4 | |||||
| q = 2**12 | |||||
| frodo_distribution = [] | |||||
| D_s = {-1: RR(1 / 3), 0: RR(1 / 3), 1: RR(1 / 3)} | |||||
| elif params == 'NIST1': | |||||
| # NIST1 FRODOKEM-640 | |||||
| n = 640 | |||||
| m = 640 | |||||
| q = 2**15 | |||||
| frodo_distribution = [9288, 8720, 7216, 5264, 3384, | |||||
| 1918, 958, 422, 164, 56, 17, 4, 1] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_NIST1.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_NIST1.sage") | |||||
| elif params == 'NIST2': | |||||
| # NIST2 FRODOKEM-976 | |||||
| n = 976 | |||||
| m = 976 | |||||
| q = 65536 | |||||
| frodo_distribution = [11278, 10277, 7774, 4882, 2545, 1101, | |||||
| 396, 118, 29, 6, 1] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_NIST2.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_NIST2.sage") | |||||
| elif params == 'CCS1': | |||||
| n = 352 | |||||
| m = 352 | |||||
| q = 2 ** 11 | |||||
| frodo_distribution = [22528, 15616, 5120, 768] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_CCS1.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_CCS1.sage") | |||||
| elif params == 'CCS2': | |||||
| n = 592 | |||||
| m = 592 | |||||
| q = 2 ** 12 | |||||
| frodo_distribution = [25120, 15840, 3968, 384, 16] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_CCS2.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_CCS2.sage") | |||||
| elif params == 'CCS3': | |||||
| n = 752 | |||||
| m = 752 | |||||
| q = 2 ** 15 | |||||
| frodo_distribution = [19296, 14704, 6496, 1664, 240, 16] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_CCS3.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_CCS3.sage") | |||||
| elif params == 'CCS4': | |||||
| n = 864 | |||||
| m = 864 | |||||
| q = 2 ** 15 | |||||
| frodo_distribution = [19304, 14700, 6490, 1659, 245, 21, 1] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_CCS4.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_CCS4.sage") | |||||
| """ Original Security """ | |||||
| A, b, dbdd = initialize_from_LWE_instance(DBDD_predict_diag, | |||||
| n, | |||||
| q, m, D_s, D_s, verbosity=0) | |||||
| dbdd.integrate_q_vectors(q, indices=range(n, n + m)) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| logging("Attack without hints: %3.2f bikz" % beta, style="HEADER") | |||||
| """ Refined Side channel attack """ | |||||
| def simu_measured(secret): | |||||
| """ | |||||
| This fonction simulates the information gained by | |||||
| Bos et al attack. The simulation is based on a | |||||
| distribution obtained with a large amount of data | |||||
| for Bos et al suite (in Matlab). | |||||
| :secret: an integer being the secret value | |||||
| :measurement: an integer that represents the output | |||||
| of Bos et al attack. | |||||
| """ | |||||
| secret = recenter(secret) | |||||
| distrib_of_guesses = renormalize_dist(Dguess[secret]) | |||||
| measurement = draw_from_distribution(distrib_of_guesses) | |||||
| return measurement | |||||
| def ordered_indices(sorted_guesses, measured): | |||||
| """ | |||||
| Necessary for the bruteforce attack, this function | |||||
| sorts the indices of the coefficients | |||||
| of the secret with decreasing likelihood. | |||||
| :sorted_guess: the best guesses in order of likelihood | |||||
| :measured: the measurement for each coefficient | |||||
| :orderered_coefficients: the indices of the coefficients | |||||
| ordered according to Probability[secret[i] = measured[i]] | |||||
| """ | |||||
| orderered_coefficients = [] | |||||
| for x in sorted_guesses: | |||||
| for i in range(len(measured)): | |||||
| meas = measured[i] | |||||
| if meas == x: | |||||
| orderered_coefficients += [i] | |||||
| return orderered_coefficients | |||||
| def estimate_SCA(report_every, dbdd, measured, max_guesses): | |||||
| """ | |||||
| This function evaluates the security loss after Bos et al attack | |||||
| :report_every: an integer that give the frequency of | |||||
| logging (None for no logging) | |||||
| :dbdd: instance of the class DBDD | |||||
| :measured: table representing the (simulated) information | |||||
| given by Bos et al attack | |||||
| :max_guesses: integer for upperbounding the number of guesses | |||||
| """ | |||||
| Id = identity_matrix(n + m) | |||||
| for i in range(n): | |||||
| v = vec(Id[i]) | |||||
| if report_every is not None and ((i % report_every == 0) or (i == n - 1)) : | |||||
| verbose = 2 | |||||
| else: | |||||
| verbose = 0 | |||||
| dbdd.verbosity = verbose | |||||
| if verbose == 2: | |||||
| logging("[...%d]" % report_every, newline=False) | |||||
| if variance_aposteriori[measured[i]] is not None and variance_aposteriori[measured[i]] != 0: | |||||
| dbdd.integrate_approx_hint(v, | |||||
| center_aposteriori[measured[i]], | |||||
| variance_aposteriori[measured[i]], | |||||
| aposteriori=True, estimate=verbose) | |||||
| elif variance_aposteriori[measured[i]] is not None and variance_aposteriori[measured[i]] == 0 : | |||||
| dbdd.integrate_perfect_hint(v, center_aposteriori[measured[i]], | |||||
| estimate=verbose) | |||||
| if report_every is not None: | |||||
| dbdd.integrate_q_vectors(q, indices=range(n, n + m), report_every=report_every) | |||||
| else: | |||||
| dbdd.integrate_q_vectors(q, indices=range(n, n + m)) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| if report_every is not None: | |||||
| logging(" Hybrid attack estimation ", style="HEADER") | |||||
| sorted_guesses = sorted(proba_best_guess_correct.items(), | |||||
| key=lambda kv: - kv[1]) | |||||
| sorted_guesses = [sorted_guesses[i][0] for i in range(len(sorted_guesses)) | |||||
| if sorted_guesses[i][1] != 1.] | |||||
| proba_success = 1. | |||||
| dbdd.verbosity = 0 | |||||
| guesses = 0 | |||||
| j = 0 | |||||
| for i in ordered_indices(sorted_guesses, measured): | |||||
| j += 1 | |||||
| if (guesses <= max_guesses): | |||||
| v = vec(Id[i]) | |||||
| if dbdd.integrate_perfect_hint(v, _): | |||||
| guesses += 1 | |||||
| proba_success *= proba_best_guess_correct[measured[i]] | |||||
| if report_every is not None and (j % report_every == 0): | |||||
| logging("[...%d]" % report_every, newline=False) | |||||
| dbdd.integrate_q_vectors(q, indices=range(n, n + m)) | |||||
| logging("dim=%3d \t delta=%.6f \t beta=%3.2f \t guesses=%4d" % | |||||
| (dbdd.dim(), dbdd.delta, dbdd.beta, guesses), | |||||
| style="VALUE", newline=False) | |||||
| logging("Proba success = %s" % proba_success, style="VALUE", | |||||
| newline=True) | |||||
| dbdd.attack() | |||||
| return beta, dbdd.beta, proba_success | |||||
| """ Example | |||||
| Uncomment the following to get the detailed computation | |||||
| """ | |||||
| A, b, dbdd = initialize_from_LWE_instance(DBDD, | |||||
| n, | |||||
| q, m, D_s, D_s, verbosity=2) | |||||
| measured = [simu_measured(dbdd.u[0, i]) for i in range(n)] | |||||
| estimate_SCA(50, dbdd, measured, 200) | |||||
+ 230
- 0
Sec6_applications/exploiting_SCA_from_Bos_et_al.sage
Прегледај датотеку
| load("../framework/instance_gen.sage") | |||||
| demo = False | |||||
| """ Example | |||||
| Uncomment the following to get an example | |||||
| of the detailed computation (without redundancy) | |||||
| """ | |||||
| demo = True | |||||
| logging("--- Demonstration mode (no averaging) ---") | |||||
| for params in ['CCS1', 'CCS2', 'CCS3', 'CCS4', 'NIST1', 'NIST2']: | |||||
| logging("Set of parameters: " + params) | |||||
| if params == 'NIST1': | |||||
| # NIST1 FRODOKEM-640 | |||||
| n = 640 | |||||
| m = 640 | |||||
| q = 2**15 | |||||
| frodo_distribution = [9288, 8720, 7216, 5264, 3384, | |||||
| 1918, 958, 422, 164, 56, 17, 4, 1] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_NIST1.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_NIST1.sage") | |||||
| elif params == 'NIST2': | |||||
| # NIST2 FRODOKEM-976 | |||||
| n = 976 | |||||
| m = 976 | |||||
| q = 65536 | |||||
| frodo_distribution = [11278, 10277, 7774, 4882, 2545, 1101, | |||||
| 396, 118, 29, 6, 1] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_NIST2.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_NIST2.sage") | |||||
| elif params == 'CCS1': | |||||
| n = 352 | |||||
| m = 352 | |||||
| q = 2 ** 11 | |||||
| frodo_distribution = [22528, 15616, 5120, 768] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_CCS1.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_CCS1.sage") | |||||
| elif params == 'CCS2': | |||||
| n = 592 | |||||
| m = 592 | |||||
| q = 2 ** 12 | |||||
| frodo_distribution = [25120, 15840, 3968, 384, 16] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_CCS2.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_CCS2.sage") | |||||
| elif params == 'CCS3': | |||||
| n = 752 | |||||
| m = 752 | |||||
| q = 2 ** 15 | |||||
| frodo_distribution = [19296, 14704, 6496, 1664, 240, 16] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_CCS3.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_CCS3.sage") | |||||
| elif params == 'CCS4': | |||||
| n = 864 | |||||
| m = 864 | |||||
| q = 2 ** 15 | |||||
| frodo_distribution = [19304, 14700, 6490, 1659, 245, 21, 1] | |||||
| D_s = get_distribution_from_table(frodo_distribution, 2 ** 16) | |||||
| load("Frodo_Single_data/simulation_distribution_CCS4.sage") | |||||
| load("Frodo_Single_data/aposteriori_distribution_CCS4.sage") | |||||
| """ Original Security """ | |||||
| A, b, dbdd = initialize_from_LWE_instance(DBDD_predict_diag, | |||||
| n, | |||||
| q, m, D_s, D_s, verbosity=0) | |||||
| dbdd.integrate_q_vectors(q, indices=range(n, n + m)) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| logging("Attack without hints: %3.2f bikz" % beta, style="HEADER") | |||||
| """ Refined Side channel attack """ | |||||
| def simu_measured(secret): | |||||
| """ | |||||
| This fonction simulates the information gained by | |||||
| Bos et al attack. The simulation is based on a | |||||
| distribution obtained with a large amount of data | |||||
| for Bos et al suite (in Matlab). | |||||
| :secret: an integer being the secret value | |||||
| :measurement: an integer that represents the output | |||||
| of Bos et al attack. | |||||
| """ | |||||
| secret = recenter(secret) | |||||
| distrib_of_guesses = renormalize_dist(Dguess[secret]) | |||||
| measurement = draw_from_distribution(distrib_of_guesses) | |||||
| return measurement | |||||
| def ordered_indices(sorted_guesses, measured): | |||||
| """ | |||||
| Necessary for the bruteforce attack, this function | |||||
| sorts the indices of the coefficients | |||||
| of the secret with decreasing likelihood. | |||||
| :sorted_guess: the best guesses in order of likelihood | |||||
| :measured: the measurement for each coefficient | |||||
| :orderered_coefficients: the indices of the coefficients | |||||
| ordered according to Probability[secret[i] = measured[i]] | |||||
| """ | |||||
| orderered_coefficients = [] | |||||
| for x in sorted_guesses: | |||||
| for i in range(len(measured)): | |||||
| meas = measured[i] | |||||
| if meas == x: | |||||
| orderered_coefficients += [i] | |||||
| return orderered_coefficients | |||||
| def estimate_SCA(report_every, dbdd, measured, max_guesses): | |||||
| """ | |||||
| This function evaluates the security loss after Bos et al attack | |||||
| :report_every: an integer that give the frequency of | |||||
| logging (None for no logging) | |||||
| :dbdd: instance of the class DBDD | |||||
| :measured: table representing the (simulated) information | |||||
| given by Bos et al attack | |||||
| :max_guesses: integer for upperbounding the number of guesses | |||||
| """ | |||||
| Id = identity_matrix(n + m) | |||||
| for i in range(n): | |||||
| v = vec(Id[i]) | |||||
| if report_every is not None and ((i % report_every == 0) or (i == n - 1)) : | |||||
| verbose = 2 | |||||
| else: | |||||
| verbose = 0 | |||||
| dbdd.verbosity = verbose | |||||
| if verbose == 2: | |||||
| logging("[...%d]" % report_every, newline=False) | |||||
| if variance_aposteriori[measured[i]] is not None and variance_aposteriori[measured[i]] != 0: | |||||
| dbdd.integrate_approx_hint(v, | |||||
| center_aposteriori[measured[i]], | |||||
| variance_aposteriori[measured[i]], | |||||
| aposteriori=True, estimate=verbose) | |||||
| elif variance_aposteriori[measured[i]] is not None and variance_aposteriori[measured[i]] == 0 : | |||||
| dbdd.integrate_perfect_hint(v, center_aposteriori[measured[i]], | |||||
| estimate=verbose) | |||||
| if report_every is not None: | |||||
| dbdd.integrate_q_vectors(q, indices=range(n, n + m), report_every=report_every) | |||||
| else: | |||||
| dbdd.integrate_q_vectors(q, indices=range(n, n + m)) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| if report_every is not None: | |||||
| logging(" Hybrid attack estimation ", style="HEADER") | |||||
| sorted_guesses = sorted(proba_best_guess_correct.items(), | |||||
| key=lambda kv: - kv[1]) | |||||
| sorted_guesses = [sorted_guesses[i][0] for i in range(len(sorted_guesses)) | |||||
| if sorted_guesses[i][1] != 1.] | |||||
| proba_success = 1. | |||||
| dbdd.verbosity = 0 | |||||
| guesses = 0 | |||||
| j = 0 | |||||
| for i in ordered_indices(sorted_guesses, measured): | |||||
| j += 1 | |||||
| if (guesses <= max_guesses): | |||||
| v = vec(Id[i]) | |||||
| if dbdd.integrate_perfect_hint(v, _): | |||||
| guesses += 1 | |||||
| proba_success *= proba_best_guess_correct[measured[i]] | |||||
| if report_every is not None and (j % report_every == 0): | |||||
| logging("[...%d]" % report_every, newline=False) | |||||
| dbdd.integrate_q_vectors(q, indices=range(n, n + m)) | |||||
| logging("dim=%3d \t delta=%.6f \t beta=%3.2f \t guesses=%4d" % | |||||
| (dbdd.dim(), dbdd.delta, dbdd.beta, guesses), | |||||
| style="VALUE", newline=False) | |||||
| logging("Proba success = %s" % proba_success, style="VALUE", | |||||
| newline=True) | |||||
| return beta, dbdd.beta, proba_success | |||||
| if demo: | |||||
| A, b, dbdd = initialize_from_LWE_instance(DBDD_predict_diag, | |||||
| n, | |||||
| q, m, D_s, D_s, verbosity=2) | |||||
| measured = [simu_measured(dbdd.u[0, i]) for i in range(n)] | |||||
| estimate_SCA(50, dbdd, measured, 200) | |||||
| else: | |||||
| """ Averaging | |||||
| The following averages the measures to get accurate data | |||||
| for the paper. The averaging mode is quite long. | |||||
| """ | |||||
| nb_tests_per_params = 100 | |||||
| # Chosen values for the number of guesses | |||||
| if params == 'CCS1': | |||||
| max_guesses = 100 | |||||
| elif params == 'CCS2': | |||||
| max_guesses = 350 | |||||
| elif params == 'CCS3': | |||||
| max_guesses = 300 | |||||
| elif params == 'CCS4': | |||||
| max_guesses = 150 | |||||
| elif params == 'NIST1': | |||||
| max_guesses = 50 | |||||
| elif params == 'NIST2': | |||||
| max_guesses = 100 | |||||
| beta = 0 | |||||
| beta_hybrid = 0 | |||||
| proba_success = 0 | |||||
| for i in range(nb_tests_per_params): | |||||
| A, b, dbdd = initialize_from_LWE_instance(DBDD_predict_diag, | |||||
| n, | |||||
| q, m, D_s, D_s, verbosity=0) | |||||
| measured = [simu_measured(dbdd.u[0, i]) for i in range(n)] | |||||
| b, b_hybrid, p_success = estimate_SCA(None, dbdd, | |||||
| measured, max_guesses) | |||||
| beta += b | |||||
| beta_hybrid += b_hybrid | |||||
| proba_success += p_success | |||||
| beta /= nb_tests_per_params | |||||
| beta_hybrid /= nb_tests_per_params | |||||
| proba_success /= nb_tests_per_params | |||||
| logging("Attack with hints: %3.2f bikz" % beta, style="HEADER") | |||||
| logging("Attack with hints and guess: %3.2f bikz"% beta_hybrid, style="HEADER") | |||||
| logging("Number of guesses: %4d" % max_guesses, style="HEADER") | |||||
| logging("Success probability: %3.2f" %proba_success, style="HEADER") |
+ 47
- 0
Sec6_applications/exploiting_decryption_failures.sage
Прегледај датотеку
| load("../framework/instance_gen.sage") | |||||
| verbosity = 0 | |||||
| report_every = None | |||||
| """ Example | |||||
| Uncomment the following to get the detailed computation | |||||
| """ | |||||
| # verbosity = 2 | |||||
| # report_every = 20 | |||||
| # FRODOKEM parameters | |||||
| n = 976 | |||||
| m = 976 | |||||
| q = 2**16 | |||||
| t = q / 16 | |||||
| D_s = {- 10: 1.52587890625e-05, - 9: 9.1552734375e-05, - 8: 0.0004425048828125, | |||||
| - 7: 0.001800537109375, - 6: 0.00604248046875, - 5: 0.0167999267578125, | |||||
| - 4: 0.0388336181640625, - 3: 0.074493408203125, - 2: 0.118621826171875, | |||||
| - 1: 0.1568145751953125, 0: 0.172088623046875, 1: 0.1568145751953125, | |||||
| 2: 0.118621826171875, 3: 0.074493408203125, 4: 0.0388336181640625, | |||||
| 5: 0.0167999267578125, 6: 0.00604248046875, 7: 0.001800537109375, | |||||
| 8: 0.0004425048828125, 9: 9.1552734375e-05, 10: 1.52587890625e-05} | |||||
| D_e = D_s | |||||
| _, var = average_variance(D_s) | |||||
| d = n + m | |||||
| ell = RR(sqrt(d * var)) | |||||
| # nu2 = RR(var * ell**4 / (t**2)) | |||||
| # for k in [0, 1, 2, 4, 8, 16, 32, 64, 128, 256]: | |||||
| # xx = 1 / (1 / var + k / nu2) | |||||
| # print(k, RR(xx / var)) | |||||
| covh = RR(var * ell**4 / (t**2)) * identity_matrix(d) | |||||
| _, _, inst = initialize_from_LWE_instance(DBDD_predict_diag, n, q, | |||||
| m, D_e, D_s, verbosity=verbosity) | |||||
| print("# failures, relative variance, bit-security (1 bit = 0.265 bikz) ") | |||||
| for i in range(0, 256): | |||||
| if report_every is not None: | |||||
| inst.integrate_q_vectors(q, indices=range(d), | |||||
| report_every=report_every) | |||||
| else: | |||||
| inst.integrate_q_vectors(q, indices=range(d)) | |||||
| print(i, ",\t \t \t", inst.S[0] / var, ",\t \t \t", inst.beta * .265) | |||||
| inst.integrate_approx_hint_fulldim(None, covh) |
+ 75
- 0
Sec6_applications/exploiting_design_LAC.sage
Прегледај датотеку
| #!/usr/bin/sage -python | |||||
| # -*- coding: latin-1 -*- | |||||
| load("../framework/instance_gen.sage") | |||||
| verbosity = 0 | |||||
| report_every = None | |||||
| """ Example | |||||
| Uncomment the following to get the detailed computation | |||||
| """ | |||||
| # verbosity = 2 | |||||
| # report_every = 50 | |||||
| for params in ['LAC-128', 'LAC-192', 'LAC-256']: | |||||
| logging("Set of parameters: " + params) | |||||
| if params == 'LAC-128': | |||||
| n = 512 | |||||
| m = 512 | |||||
| q = 251 | |||||
| D_e = {-1: 0.25, 0: 0.5, 1: 0.25} | |||||
| D_s = D_e | |||||
| elif params == 'LAC-192': | |||||
| n = 1024 | |||||
| m = 1024 | |||||
| q = 251 | |||||
| D_e = {-1: 0.125, 0: 0.75, 1: 0.125} | |||||
| D_s = D_e | |||||
| elif params == 'LAC-256': | |||||
| n = 1024 | |||||
| m = 1024 | |||||
| q = 251 | |||||
| D_e = {-1: 0.25, 0: 0.5, 1: 0.25} | |||||
| D_s = D_e | |||||
| # Assessement of the attack without hints | |||||
| A, b, dbdd = initialize_LAC_instance(DBDD_predict_diag, n, q, | |||||
| m, D_e, D_s, | |||||
| verbosity=verbosity) | |||||
| if report_every is not None: | |||||
| dbdd.integrate_q_vectors(q, indices=range(0, n + m), report_every=report_every) | |||||
| else: | |||||
| dbdd.integrate_q_vectors(q, indices=range(0, n + m)) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| logging("Attack without hints: %3.2f bikz" % beta, style="HEADER") | |||||
| # Assessement of the attack with hints | |||||
| A, b, dbdd = initialize_LAC_instance(DBDD_predict, n, q, | |||||
| m, D_e, D_s, | |||||
| verbosity=verbosity) | |||||
| v = vec([1 if i < m else 0 for i in range(m + n)]) | |||||
| dbdd.integrate_perfect_hint(v, 0) | |||||
| v = vec([0 if i < m else 1 for i in range(m + n)]) | |||||
| dbdd.integrate_perfect_hint(v, 0) | |||||
| M = q * identity_matrix(n + m) | |||||
| i = 0 | |||||
| V = vec(M[0] - M[1]) | |||||
| logging("[...%d]" % report_every, newline=False) | |||||
| while dbdd.integrate_short_vector_hint(V): | |||||
| if report_every is not None and ((i % report_every == 0) or (i == m - 1)): | |||||
| verbose = 2 | |||||
| else: | |||||
| verbose = 0 | |||||
| dbdd.verbosity = verbose | |||||
| if verbose == 2: | |||||
| logging("[...%d]" % report_every, newline=False) | |||||
| i += 1 | |||||
| V = vec(M[i] - M[i + 1]) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| logging("Attack with hints: %3.2f bikz" % beta, style="HEADER") |
+ 75
- 0
Sec6_applications/exploiting_design_ntru.sage
Прегледај датотеку
| #!/usr/bin/sage -python | |||||
| # -*- coding: latin-1 -*- | |||||
| load("../framework/instance_gen.sage") | |||||
| verbosity = 0 | |||||
| report_every = None | |||||
| """ Example | |||||
| Uncomment the following to get the detailed computation | |||||
| """ | |||||
| # verbosity = 2 | |||||
| # report_every = 20 | |||||
| for params in [ 'ntruhps2048509', 'ntruhps2048677', 'ntruhps4096821']: | |||||
| logging("Set of parameters: " + params) | |||||
| if params == 'ntruhps2048509': | |||||
| n = 509 | |||||
| m = 509 | |||||
| q = 2048 | |||||
| elif params == 'ntruhps2048677': | |||||
| n = 677 | |||||
| m = 677 | |||||
| q = 2048 | |||||
| elif params == 'ntruhps4096821': | |||||
| n = 821 | |||||
| m = 821 | |||||
| q = 4096 | |||||
| hamming_weight = (q / 16 - 1) | |||||
| if q / 8 - 2 <= 2 * n / 3: | |||||
| hamming_weight = (q / 16 - 1) | |||||
| else: | |||||
| hamming_weight = floor(n / 3) | |||||
| D_s = {- 1: RR(hamming_weight / n), | |||||
| 0: 1 - RR(2 * hamming_weight / n), | |||||
| 1: RR(hamming_weight / n)} | |||||
| # D_e = {- 1: RR(hamming_weight / n), | |||||
| # 0: 1 - RR(2 * hamming_weight / n), | |||||
| # 1: RR(hamming_weight / n)} | |||||
| D_e = {-1: RR(1 / 3), 0: RR(1 / 3), 1: RR(1 / 3)} | |||||
| # Assessement of the attack without hints | |||||
| A, b, dbdd = initialize_NTRU_instance(DBDD_predict_diag, | |||||
| n, q, m, D_e, D_s, | |||||
| verbosity=verbosity) | |||||
| if report_every is not None: | |||||
| dbdd.integrate_q_vectors(q, indices=range(0, n + m), report_every=report_every) | |||||
| else: | |||||
| dbdd.integrate_q_vectors(q, indices=range(0, n + m)) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| logging("Attack without hints: %3.2f bikz" % beta, style="HEADER") | |||||
| # Assessement of the attack with hints | |||||
| A, b, dbdd = initialize_NTRU_instance(DBDD_predict, | |||||
| n, q, m, D_e, D_s, | |||||
| verbosity=verbosity) | |||||
| v = vec([0 if i < m else 1 for i in range(m + n)]) | |||||
| dbdd.integrate_perfect_hint(v, 0) | |||||
| if report_every is not None: | |||||
| dbdd.integrate_q_vectors(q, indices=range(0, m), report_every=report_every) | |||||
| else: | |||||
| dbdd.integrate_q_vectors(q, indices=range(0, m)) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| logging("Attack without hints: %3.2f bikz" % beta, style="HEADER") |
+ 78
- 0
Sec6_applications/exploiting_design_ntru_prime.sage
Прегледај датотеку
| #!/usr/bin/sage -python | |||||
| # -*- coding: latin-1 -*- | |||||
| load("../framework/instance_gen.sage") | |||||
| verbosity = 0 | |||||
| report_every = None | |||||
| """ Example | |||||
| Uncomment the following to get the detailed computation | |||||
| """ | |||||
| # verbosity = 2 | |||||
| # report_every = 50 | |||||
| for params in ['kem/sntrup653', 'kem/sntrup761', 'kem/sntrup857']: | |||||
| logging("Set of parameters: " + params) | |||||
| if params == 'kem/sntrup653': | |||||
| n = 653 | |||||
| m = n | |||||
| q = 4621 | |||||
| w = 288 | |||||
| elif params == 'kem/sntrup761': | |||||
| n = 761 | |||||
| m = n | |||||
| q = 4591 | |||||
| w = 286 | |||||
| elif params == 'kem/sntrup857': | |||||
| n = 857 | |||||
| m = n | |||||
| q = 5167 | |||||
| w = 322 | |||||
| elif params == 'kem/ntrulpr653': | |||||
| n = 653 | |||||
| m = n | |||||
| q = 4621 | |||||
| w = 252 | |||||
| elif params == 'kem/ntrulpr761': | |||||
| n = 761 | |||||
| m = n | |||||
| q = 4591 | |||||
| w = 250 | |||||
| elif params == 'kem/ntrulpr857': | |||||
| n = 857 | |||||
| m = n | |||||
| q = 5167 | |||||
| w = 281 | |||||
| D_f = {-1: RR(w / n / 2), 0: 1 - RR(w / n), 1: RR(w / n / 2)} | |||||
| D_g = {-1: RR(1 / 3), 0: RR(1 / 3), 1: RR(1 / 3)} | |||||
| only_predictions = True | |||||
| A, b, dbdd = initialize_NTRU_prime_instance(DBDD_predict_diag, n, q, m, w, D_f, D_g, verbosity=verbosity) | |||||
| if report_every is not None: | |||||
| dbdd.integrate_q_vectors(q, report_every=report_every) | |||||
| else: | |||||
| dbdd.integrate_q_vectors(q) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| logging("Attack without hints: %3.2f bikz" % beta, style="HEADER") | |||||
| A, b, dbdd = initialize_NTRU_prime_instance(DBDD_predict, n, q, m, w, D_f, D_g, verbosity=verbosity) | |||||
| v = vec([1 if i < m else 0 for i in range(m + n)]) | |||||
| dbdd.integrate_modular_hint(v, w, 2, True) | |||||
| if report_every is not None: | |||||
| dbdd.integrate_q_vectors(q, report_every=report_every) | |||||
| else: | |||||
| dbdd.integrate_q_vectors(q) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| logging("Attack with hints: %3.2f bikz" % beta, style="HEADER") |
+ 70
- 0
Sec6_applications/exploiting_design_round5.sage
Прегледај датотеку
| #!/usr/bin/sage -python | |||||
| # -*- coding: latin-1 -*- | |||||
| load("../framework/instance_gen.sage") | |||||
| verbosity = 0 | |||||
| report_every = None | |||||
| """ Example | |||||
| Uncomment the following to get the detailed computation | |||||
| """ | |||||
| # verbosity = 2 | |||||
| # report_every = 20 | |||||
| for params in ['R5ND_{1}KEM_0d', 'R5ND_{3}KEM_0d', 'R5ND_{5}KEM_0d']: | |||||
| logging("Set of parameters: " + params) | |||||
| if params == 'R5ND_{1}KEM_0d': | |||||
| n = 618 | |||||
| m = 618 | |||||
| q = 2 ** 11 | |||||
| p = 2 ** 8 | |||||
| h = 104 | |||||
| elif params == 'R5ND_{3}KEM_0d': | |||||
| n = 786 | |||||
| m = 786 | |||||
| q = 2 ** 13 | |||||
| p = 2 ** 9 | |||||
| h = 384 | |||||
| elif params == 'R5ND_{5}KEM_0d': | |||||
| n = 1018 | |||||
| m = 1018 | |||||
| q = 2 ** 14 | |||||
| p = 2 ** 9 | |||||
| h = 428 | |||||
| D_s = {-1: RR(h / 2 / n), 0: RR((n - h) / n), 1: RR(h / 2 / n)} | |||||
| D_e = build_uniform_law(q / p) | |||||
| # Assessement of the attack without hints | |||||
| A, b, dbdd = initialize_round5_instance(DBDD_predict_diag, n, | |||||
| q, p, h, m, D_e, D_s, | |||||
| verbosity=verbosity) | |||||
| if report_every is not None: | |||||
| dbdd.integrate_q_vectors(q, indices=range(0, n + m), | |||||
| report_every=report_every) | |||||
| else: | |||||
| dbdd.integrate_q_vectors(q, indices=range(0, n + m)) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| logging("Attack without hints: %3.2f bikz" % beta, style="HEADER") | |||||
| # Assessement of the attack with hints | |||||
| A, b, dbdd = initialize_round5_instance(DBDD_predict, n, | |||||
| q, p, h, m, D_e, D_s, | |||||
| verbosity=verbosity) | |||||
| v = vec([0 if i < m else 1 for i in range(m + n)]) | |||||
| dbdd.integrate_perfect_hint(v, 0) | |||||
| if report_every is not None: | |||||
| dbdd.integrate_q_vectors(q, indices=range(0, m), report_every=report_every) | |||||
| else: | |||||
| dbdd.integrate_q_vectors(q, indices=range(0, m)) | |||||
| (beta, _) = dbdd.estimate_attack() | |||||
| logging("Attack without hints: %3.2f bikz" % beta, style="HEADER") |
+ 9
- 0
Sec6_applications/run_all_applications.sage
Прегледај датотеку
| print("Generating all data (takes a while...)") | |||||
| print("\nFor Table 3\n") | |||||
| load("exploiting_SCA_from_Bos_et_al.sage") | |||||
| print("\nFor Figure 6\n") | |||||
| load("exploiting_decryption_failures.sage") | |||||
| print("\nFor Table 4 \n") | |||||
| load("exploiting_design_LAC.sage") | |||||
| load("exploiting_design_ntru.sage") | |||||
| load("exploiting_design_round5.sage") |
+ 384
- 0
framework/DBDD.sage
Прегледај датотеку
| from fpylll import * | |||||
| from fpylll.algorithms.bkz2 import BKZReduction | |||||
| load("../framework/load_strategies.sage") | |||||
| load("../framework/DBDD_generic.sage") | |||||
| load("../framework/proba_utils.sage") | |||||
| # Restoration Type | |||||
| SUBSTITUTION = 0 | |||||
| QMODULUS_SUBSTITUTION = 1 | |||||
| class DBDD(DBDD_generic): | |||||
| """ | |||||
| This class defines all the elements defining a DBDD instance with all | |||||
| the basis computations | |||||
| """ | |||||
| def __init__(self, B, S, mu, u=None, verbosity=1, float_type="ld", **kwargs): | |||||
| """constructor that builds a DBDD instance from a lattice, mean, sigma | |||||
| and a target | |||||
| ;min_dim: Number of coordinates to find to consider the problem solved | |||||
| :B: Basis of the lattice | |||||
| :S: The Covariance matrix (Sigma) of the uSVP solution | |||||
| :mu: The expectation of the uSVP solution | |||||
| :u: The unique vector to be found (optinal, for verification purposes) | |||||
| :fp_type: Floating point type to use in FPLLL ("d, ld, dd, qd") | |||||
| """ | |||||
| self.verbosity = verbosity | |||||
| self.B = B # The lattice Basis | |||||
| self.D = kwargs.get('D', None) # The dual Basis (only B or D is active) | |||||
| assert self.D.T * self.B == identity_matrix(B.nrows()) | |||||
| self._dim = B.nrows() | |||||
| #self._keep_basis = False | |||||
| self.S = S | |||||
| self.PP = 0 * S # Span of the projections so far (orthonormal) | |||||
| self.mu = mu | |||||
| self.u = u | |||||
| self.u_original = u | |||||
| self.expected_length = RR(sqrt(self.S.trace()) + 1) | |||||
| self.projections = 0 | |||||
| self.save = {"save": None} | |||||
| self.float_type = float_type | |||||
| self.estimate_attack(silent=True) | |||||
| self.Pi = identity_matrix(self._dim) # Reduction matrix | |||||
| self.Gamma = identity_matrix(self._dim) # Substitution matrix | |||||
| self._restoration_instructions = [] | |||||
| def dim(self): | |||||
| return self._dim | |||||
| def S_diag(self): | |||||
| return [self.S[i, i] for i in range(self.S.nrows())] | |||||
| @without_dependencies | |||||
| def volumes(self): | |||||
| if self.B is not None: | |||||
| Bvol = logdet(self.B * self.B.T) / 2 | |||||
| else: | |||||
| Bvol = -logdet(self.D * self.D.T) / 2 | |||||
| S = self.S + self.mu.T * self.mu | |||||
| Svol = degen_logdet(S) | |||||
| dvol = Bvol - Svol / 2. | |||||
| return (Bvol, Svol, dvol) | |||||
| @without_dependencies | |||||
| def test_primitive_dual(self, V, action): | |||||
| if self.B is None: | |||||
| self.B = dual_basis(self.D) | |||||
| W = V * self.B.T | |||||
| den = lcm([x.denominator() for x in W[0]]) | |||||
| num = gcd([x for x in W[0] * den]) | |||||
| assert den == 1 | |||||
| if num == 1: | |||||
| return True | |||||
| if action == "warn": | |||||
| logging("non-primitive (factor %d)." % | |||||
| num, style="WARNING", newline=False) | |||||
| return True | |||||
| elif action == "reject": | |||||
| raise RejectedHint("non-primitive (factor %d)." % num) | |||||
| raise InvalidHint("non-primitive (factor %d)." % num) | |||||
| def get_reduced_hint_vector(self, V): | |||||
| V = V * self.Gamma | |||||
| if V == 0: | |||||
| raise RejectedHint("Redundant hint") | |||||
| return V | |||||
| def add_restoration_instruction(self, type, Gamma, **data): | |||||
| self.Gamma *= Gamma | |||||
| last_instruction = self._restoration_instructions[-1] if len(self._restoration_instructions)>0 else (None, None, None) | |||||
| if type==SUBSTITUTION and last_instruction is not None and last_instruction[0]==SUBSTITUTION: | |||||
| self._restoration_instructions[-1] = (SUBSTITUTION, last_instruction[1]*Gamma, {}) | |||||
| else: | |||||
| self._restoration_instructions.append((type, Gamma, data)) | |||||
| #@not_after_projections | |||||
| #@hint_integration_wrapper(force=True, requires=["dual"], invalidates=["primal"]) | |||||
| #def reduce_dimension(self, Gamma, normalization_matrix=None): | |||||
| # if normalization_matrix is None: | |||||
| # normalization_matrix = (Gamma.T * Gamma).inverse() | |||||
| # normalized_Gamma = Gamma*normalization_matrix | |||||
| # | |||||
| # self.D = self.D * Gamma | |||||
| # self.mu = self.mu * normalized_Gamma | |||||
| # self.S = normalized_Gamma.T * self.S * normalized_Gamma | |||||
| # self.PP = 0 * self.S | |||||
| # | |||||
| # #self.Pi *= normalized_Gamma | |||||
| # self.add_restoration_instruction(SUBSTITUTION, Gamma) | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper(force=True, requires=["dual"], | |||||
| invalidates=["primal"]) | |||||
| def integrate_perfect_hint(self, v, l, reduction=False): | |||||
| V = concatenate(v, -l) | |||||
| V = self.get_reduced_hint_vector(V) | |||||
| VS = V * self.S | |||||
| den = scal(VS * V.T) | |||||
| if den == 0: | |||||
| raise NotImplementedError('Normally, useless condition') | |||||
| #raise RejectedHint("Redundant hint") | |||||
| self.D = lattice_orthogonal_section(self.D, V) | |||||
| self._dim -= 1 | |||||
| num = self.mu * V.T | |||||
| self.mu -= (num / den) * VS | |||||
| num = VS.T * VS | |||||
| self.S -= num / den | |||||
| ## Dimension Reduction | |||||
| Gamma, data = build_standard_substitution_matrix(V, output_data=True) | |||||
| normalization_matrix = data['normalization_matrix'] | |||||
| normalized_Gamma = Gamma*normalization_matrix | |||||
| self.D = self.D * Gamma | |||||
| self.mu = self.mu * normalized_Gamma | |||||
| self.S = normalized_Gamma.T * self.S * normalized_Gamma | |||||
| self.PP = 0 * self.S | |||||
| self.Pi = normalized_Gamma.T * self.Pi | |||||
| self.add_restoration_instruction(SUBSTITUTION, Gamma) | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper(force=True, requires=["dual"], invalidates=["primal"]) | |||||
| def integrate_modular_hint(self, v, l, k, smooth=True): | |||||
| V = concatenate(v, -l) | |||||
| V = self.get_reduced_hint_vector(V) | |||||
| VS = V * self.S | |||||
| den = scal(VS * V.T) | |||||
| if den == 0: | |||||
| raise NotImplementedError('Normally, useless condition') | |||||
| #raise RejectedHint("Redundant hint") | |||||
| if not smooth: | |||||
| raise NotImplementedError() | |||||
| self.D = lattice_modular_intersection(self.D, V, k) | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper(force=True, requires=["dual"], invalidates=["primal"]) | |||||
| def integrate_q_modular_hint(self, v, l, q): | |||||
| V = concatenate(v, -l) | |||||
| V = self.get_reduced_hint_vector(V) | |||||
| if V == 0: | |||||
| raise RejectedHint("Redundant hint") | |||||
| _, pivot = V.nonzero_positions()[0] | |||||
| V = V * int(mod(V[0,pivot],q)**(-1)) % q | |||||
| V = V.apply_map(lambda x: recenter(x,q)) | |||||
| W = q * canonical_vec(self._dim, pivot) | |||||
| Gamma = build_standard_substitution_matrix(V, pivot=pivot) | |||||
| assert scal(V * W.T)/q == 1, f'<V, W> = {scal(V * W.T)/q} != 1' | |||||
| self.D = lattice_modular_intersection(self.D, V, q) | |||||
| # So, V/q is a dual vector, and we hope it is a primitive one | |||||
| ## Let build the reduction matrix \Pi | |||||
| #B_ = block_matrix(QQ, [[Gamma.T], [W]]) | |||||
| #Pi = dual_basis(B_)[:self._dim-1] | |||||
| dim = self._dim | |||||
| Pi = block_matrix(QQ, [ | |||||
| [identity_matrix(pivot), zero_matrix(pivot,1), zero_matrix(pivot, dim-pivot-1)], | |||||
| [zero_matrix(dim-pivot-1, pivot), zero_matrix(dim-pivot-1,1), identity_matrix(dim-pivot-1)], | |||||
| ]) | |||||
| assert Pi.dimensions() == (dim-1, dim), 'Error in the dimension of \Pi' | |||||
| assert Pi * Gamma == identity_matrix(dim-1), 'Error in the calculation of \Pi: \Pi\Gamma != I' | |||||
| assert Pi * W.T == 0, 'Error in the calculation of \Pi: \Pi W != 0' | |||||
| self._dim -= 1 | |||||
| # Even if we have a formulae for the primal basis, it is incorrect because we don't apply "lattice_modular_intersection" on self.B | |||||
| if self.D is not None: | |||||
| self.D = self.D * Gamma | |||||
| self.mu = self.mu * Pi.T | |||||
| self.S = Pi * self.S * Pi.T | |||||
| self.PP = 0 * self.S | |||||
| self.Pi = Pi * self.Pi | |||||
| self.add_restoration_instruction(QMODULUS_SUBSTITUTION, Gamma, w=W, v=V, q=q) | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper(force=True) | |||||
| def integrate_approx_hint(self, v, l, variance, aposteriori=False): | |||||
| if variance < 0: | |||||
| raise InvalidHint("variance must be non-negative !") | |||||
| if variance == 0: | |||||
| raise InvalidHint("variance=0 : must use perfect hint !") | |||||
| if not aposteriori: | |||||
| V = concatenate(v, -l) | |||||
| V = self.get_reduced_hint_vector(V) | |||||
| VS = V * self.S | |||||
| d = scal(VS * V.T) | |||||
| center = scal(self.mu * V.T) | |||||
| coeff = (- center / (variance + d)) | |||||
| self.mu += coeff * VS | |||||
| self.S -= (1 / (variance + d) * VS.T) * VS | |||||
| else: | |||||
| V = concatenate(v, 0) | |||||
| V = self.get_reduced_hint_vector(V) | |||||
| VS = V * self.S | |||||
| # test if eigenvector | |||||
| #if not scal(VS * V.T)**2 == scal(VS * VS.T) * scal(V * V.T): | |||||
| # raise RejectedHint("Not an eigenvector of Σ,") | |||||
| if not scal(VS * VS.T): | |||||
| raise RejectedHint("0-Eigenvector of Σ forbidden,") | |||||
| # New formulae | |||||
| den = scal(VS * V.T) | |||||
| self.mu += ((l - scal(self.mu * V.T)) / den) * VS | |||||
| self.S += (((variance - den) / den**2) * VS.T ) * VS | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper() | |||||
| def integrate_approx_hint_fulldim(self, center, | |||||
| covariance, aposteriori=False): | |||||
| # Using http://www.cs.columbia.edu/~liulp/pdf/linear_normal_dist.pdf | |||||
| # with A = Id | |||||
| if not aposteriori: | |||||
| d = self.S.nrows() - 1 | |||||
| if self.S.rank() != d or covariance.rank() != d: | |||||
| raise InvalidHint("Covariances not full dimensional") | |||||
| zero = vec(d * [0]) | |||||
| F = (self.S + block4(covariance, zero.T, zero, vec([1]))).inverse() | |||||
| F[-1, -1] = 0 | |||||
| C = concatenate(center, 1) | |||||
| self.mu += ((C - self.mu) * F) * self.S | |||||
| self.S -= self.S * F * self.S | |||||
| else: | |||||
| raise NotImplementedError() | |||||
| @hint_integration_wrapper(force=False, | |||||
| requires=["primal"], | |||||
| invalidates=["dual"]) | |||||
| def integrate_short_vector_hint(self, v): | |||||
| V = concatenate(v, 0) | |||||
| if V.dimensions()[1] > self._dim: | |||||
| V = V * self.Pi.T # Reduction | |||||
| assert V.dimensions()[1] == self._dim | |||||
| V -= V * self.PP | |||||
| if scal((V * self.S) * V.T) == 0: | |||||
| raise InvalidHint("Projects to 0") | |||||
| self.projections += 1 | |||||
| PV = identity_matrix(V.ncols()) - projection_matrix(V) | |||||
| try: | |||||
| self.B = lattice_project_against(self.B, V) | |||||
| self._dim -= 1 | |||||
| except ValueError: | |||||
| raise InvalidHint("Not in Λ") | |||||
| self.mu = self.mu * PV | |||||
| self.u = self.u * (self.Pi.T * PV * self.Gamma.T) | |||||
| self.S = PV.T * self.S * PV | |||||
| self.PP += V.T * (V / scal(V * V.T)) | |||||
| @without_dependencies | |||||
| def attack(self, beta_max=None, beta_pre=None, randomize=False, tours=1): | |||||
| """ | |||||
| Run the lattice reduction to solve the DBDD instance. | |||||
| Return the (blocksize, solution) of a succesful attack, | |||||
| or (None, None) on failure | |||||
| """ | |||||
| self.logging(" Running the Attack ", style="HEADER") | |||||
| if self.B is None: | |||||
| self.B = dual_basis(self.D) | |||||
| # Apply adequate distortion | |||||
| denom = lcm([x.denominator() for x in self.B.list()]) | |||||
| B = self.B | |||||
| d = B.nrows() | |||||
| S = self.S + self.mu.T * self.mu | |||||
| L, Linv = square_root_inverse_degen(S, self.B) | |||||
| M = B * Linv | |||||
| # Make the matrix Integral | |||||
| denom = lcm([x.denominator() for x in M.list()]) | |||||
| M = matrix(ZZ, M * denom) | |||||
| # Build the BKZ object | |||||
| G = None | |||||
| try: | |||||
| G = GSO.Mat(IntegerMatrix.from_matrix(M), float_type=self.float_type) | |||||
| except ValueError as e: | |||||
| G = GSO.Mat(IntegerMatrix.from_matrix(M)) | |||||
| bkz = BKZReduction(G) | |||||
| if randomize: | |||||
| bkz.lll_obj() | |||||
| bkz.randomize_block(0, d, density=d / 4) | |||||
| bkz.lll_obj() | |||||
| u_den = lcm([x.denominator() for x in self.u.list()]) | |||||
| if beta_pre is not None: | |||||
| self.logging("\rRunning BKZ-%d (until convergence)" % | |||||
| beta_pre, newline=False) | |||||
| bkz.lll_obj() | |||||
| par = BKZ.Param(block_size=beta_pre, strategies=strategies) | |||||
| bkz(par) | |||||
| bkz.lll_obj() | |||||
| else: | |||||
| beta_pre = 2 | |||||
| # Run BKZ tours with progressively increasing blocksizes | |||||
| for beta in range(beta_pre, B.nrows() + 1): | |||||
| self.logging("\rRunning BKZ-%d" % beta, newline=False) | |||||
| if beta_max is not None: | |||||
| if beta > beta_max: | |||||
| self.logging("Failure ... (reached beta_max)", | |||||
| style="SUCCESS") | |||||
| self.logging("") | |||||
| return None, None | |||||
| if beta == 2: | |||||
| bkz.lll_obj() | |||||
| else: | |||||
| par = BKZ.Param(block_size=beta, | |||||
| strategies=strategies, max_loops=tours) | |||||
| bkz(par) | |||||
| bkz.lll_obj() | |||||
| # Recover the tentative solution, | |||||
| # undo distorition, scaling, and test it | |||||
| v = vec(bkz.A[0]) | |||||
| v = u_den * v * L / denom | |||||
| solution = matrix(ZZ, v.apply_map(round)) / u_den | |||||
| self.reduced_solution = solution | |||||
| for instruc_type, Gamma, data in self._restoration_instructions[::-1]: | |||||
| solution = solution * Gamma.T | |||||
| if instruc_type == SUBSTITUTION: | |||||
| pass | |||||
| elif instruc_type == QMODULUS_SUBSTITUTION: | |||||
| solution += data['w'] * round(solution[0].inner_product(data['v'][0])/data['q']) | |||||
| else: | |||||
| solution += data['w'] * data['func'](solution) | |||||
| if not self.check_solution(solution): | |||||
| continue | |||||
| self.logging("Success !", style="SUCCESS") | |||||
| self.logging("") | |||||
| return beta, solution | |||||
| self.logging("Failure ...", style="FAILURE") | |||||
| self.logging("") | |||||
| return None, None |
+ 321
- 0
framework/DBDD_generic.sage
Прегледај датотеку
| from fpylll import * | |||||
| # current version fpylll raises a lot of Deprecation warnings. Silence that. | |||||
| import warnings | |||||
| warnings.filterwarnings("ignore", category=DeprecationWarning) | |||||
| load("../framework/proba_utils.sage") | |||||
| load("../framework/utils.sage") | |||||
| load("../framework/geometry.sage") | |||||
| # Issues with hint that are caught, and only raise a warning | |||||
| class RejectedHint(Exception): | |||||
| def __init__(self, message): | |||||
| self.message = message | |||||
| def __str__(self): | |||||
| return self.message | |||||
| # Issues with hint that are caught, and only raise a warning | |||||
| class InvalidHint(Exception): | |||||
| def __init__(self, message): | |||||
| self.message = message | |||||
| def __str__(self): | |||||
| return self.message | |||||
| def not_after_projections(fn): | |||||
| def decorated(self, *args, **kwargs): | |||||
| # if self.projections: | |||||
| # self.logging("You can't integrate more hints after projection. Sorry.", ) | |||||
| # raise ValueError | |||||
| return fn(self, *args, **kwargs) | |||||
| return decorated | |||||
| def without_dependencies(fn): | |||||
| def decorated(self, *args, **kwargs): | |||||
| has_been_reduced = False | |||||
| if self.B is not None: | |||||
| has_been_reduced = has_been_reduced or (self.B.nrows() > self._dim) | |||||
| self.B = remove_linear_dependencies(self.B, self._dim) | |||||
| if self.D is not None: | |||||
| if has_been_reduced and (self.D.nrows() > self._dim): | |||||
| self.logging("(Warning, double computation with LLL)", priority=0, style='WARNING', newline=False) | |||||
| has_been_reduced = has_been_reduced or (self.D.nrows() > self._dim) | |||||
| self.D = remove_linear_dependencies(self.D, self._dim) | |||||
| return fn(self, *args, **kwargs) | |||||
| return decorated | |||||
| def hint_integration_wrapper(force=False, | |||||
| non_primitive_action=None, | |||||
| requires=[], | |||||
| invalidates=[], | |||||
| catch_invalid_hint=True, | |||||
| estimate=True): | |||||
| def decorator(fn): | |||||
| def decorated(self, *args, **kwargs): | |||||
| if self.verbosity: | |||||
| self.logging(fn.__name__.replace("_", " "), | |||||
| style='ACTION', priority=1, newline=False) | |||||
| if fn.__name__ == "integrate_perfect_hint": | |||||
| self.logging(hint_to_string( | |||||
| args[0], args[1]), style='DATA', | |||||
| priority=2, newline=False) | |||||
| if fn.__name__ == "integrate_modular_hint": | |||||
| self.logging("(smooth)" if kwargs.get( | |||||
| "smooth", True) else "(nonsmooth)", | |||||
| priority=1, newline=False) | |||||
| self.logging(hint_to_string( | |||||
| args[0], args[1]) + " MOD %d" % args[2], style='DATA', | |||||
| priority=2, newline=False) | |||||
| if fn.__name__ == "integrate_approx_hint": | |||||
| self.logging("(aposteriori)" if kwargs.get( | |||||
| "aposteriori", False) else "(conditionning)", | |||||
| priority=1, newline=False) | |||||
| self.logging(hint_to_string( | |||||
| args[0], args[1]) + " + χ(σ²=%.3f)" % args[2], | |||||
| style='DATA', priority=2, newline=False) | |||||
| if fn.__name__ == "integrate_short_vector_hint": | |||||
| self.logging(hint_to_string( | |||||
| args[0], None, lit="c") + "∈ Λ", style='DATA', | |||||
| priority=2, newline=False) | |||||
| if "primal" in requires and self.B is None: | |||||
| self.D = remove_linear_dependencies(self.D, self._dim) | |||||
| self.B = dual_basis(self.D) | |||||
| if "dual" in requires and self.D is None: | |||||
| self.B = remove_linear_dependencies(self.B, self._dim) | |||||
| self.D = dual_basis(self.B) | |||||
| if "force" in kwargs: | |||||
| _force = kwargs["force"] | |||||
| del kwargs["force"] | |||||
| else: | |||||
| _force = force | |||||
| if "estimate" in kwargs: | |||||
| _estimate = kwargs["estimate"] | |||||
| del kwargs["estimate"] | |||||
| else: | |||||
| _estimate = estimate | |||||
| if (not _force) or _estimate: | |||||
| self.stash() | |||||
| if "catch_invalid_hint" in kwargs: | |||||
| _catch_invalid_hint = kwargs["catch_invalid_hint"] | |||||
| del kwargs["catch_invalid_hint"] | |||||
| else: | |||||
| _catch_invalid_hint = catch_invalid_hint | |||||
| if "non_primitive_action" in kwargs: | |||||
| _non_primitive_action = kwargs["non_primitive_action"] | |||||
| del kwargs["non_primitive_action"] | |||||
| else: | |||||
| _non_primitive_action = non_primitive_action | |||||
| try: | |||||
| if _non_primitive_action is not None: | |||||
| self.test_primitive_dual(concatenate( | |||||
| args[0], -args[1]), _non_primitive_action) | |||||
| fn(self, *args, **kwargs) | |||||
| self.beta = None | |||||
| except RejectedHint as err: | |||||
| logging(str(err) + ", Rejected.", style="REJECT", newline=True) | |||||
| return False | |||||
| except InvalidHint as err: | |||||
| if _catch_invalid_hint: | |||||
| logging(str(err) + ", Invalid.", | |||||
| style="REJECT", newline=True) | |||||
| return False | |||||
| else: | |||||
| raise err | |||||
| if "primal" in invalidates: | |||||
| self.B = None | |||||
| if "dual" in invalidates: | |||||
| self.D = None | |||||
| if (not _force) or _estimate: | |||||
| return self.undo_if_unworthy(_force) | |||||
| else: | |||||
| self.logging("", newline=True) | |||||
| return True | |||||
| return decorated | |||||
| return decorator | |||||
| class DBDD_generic: | |||||
| """ | |||||
| This class defines all the elements defining a DBDD instance | |||||
| """ | |||||
| def __init__(): | |||||
| raise NotImplementedError( | |||||
| "The generic class is not meant to be used directly.") | |||||
| def leak(self, v): | |||||
| value = scal(self.u * concatenate([v, [0]]).T) | |||||
| return value | |||||
| def stash(self): | |||||
| if self.beta is None: | |||||
| self.estimate_attack(silent=True) | |||||
| for key, val in self.__dict__.items(): | |||||
| if key != "save": | |||||
| self.save[key] = copy(val) | |||||
| def pop(self): | |||||
| for key, val in self.save.items(): | |||||
| if key != "save": | |||||
| self.__dict__[key] = val | |||||
| def undo_if_unworthy(self, force): | |||||
| self.estimate_attack(silent=True) | |||||
| if (-self.beta, self.delta)\ | |||||
| <= (-self.save["beta"], self.save["delta"]): | |||||
| if force: | |||||
| self.logging("\t Unworthy hint, Forced it.", style="REJECT") | |||||
| return True | |||||
| else: | |||||
| self.logging("\t Unworthy hint, Rejected.", style="REJECT") | |||||
| self.pop() | |||||
| return False | |||||
| self.logging("\t Worthy hint !", style="ACCEPT", newline=False) | |||||
| self.logging("dim=%3d, δ=%.8f, β=%3.2f" % | |||||
| (self.dim(), self.delta, self.beta), style="VALUE") | |||||
| return True | |||||
| def logging(self, message, priority=1, style='NORMAL', newline=True): | |||||
| if priority > self.verbosity: | |||||
| return | |||||
| logging(message, style=style, newline=newline) | |||||
| def check_solution(self, solution): | |||||
| """ Checks wether the solution is correct | |||||
| If the private attributes of the instance are not None, | |||||
| the solution is compared to them. It outputs True | |||||
| if the solution is indeed the same as the private s and e, | |||||
| False otherwise. | |||||
| If the private e and s are not stored, we check that the | |||||
| solution is small enough. | |||||
| :solution: a vector | |||||
| """ | |||||
| if self.u == solution or self.u == - solution: | |||||
| return True | |||||
| if scal(solution * solution.T) > 1.2 * self.expected_length: | |||||
| #print(scal(solution * solution.T), 1.2 * self.expected_length) | |||||
| return False | |||||
| if self.u is None: | |||||
| return True | |||||
| if self.verbosity: | |||||
| self.logging("Found an incorrect short solution.", | |||||
| priority=-1, style="WARNING") | |||||
| #print(solution) | |||||
| return False | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper() | |||||
| def integrate_perfect_hint(self, v, l): | |||||
| raise NotImplementedError("This method is not generic.") | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper() | |||||
| def integrate_modular_hint(self, v, l, k, smooth=True): | |||||
| raise NotImplementedError("This method is not generic.") | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper() | |||||
| def integrate_approx_hint(self, v, l, variance, aposteriori=False): | |||||
| raise NotImplementedError("This method is not generic.") | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper() | |||||
| def integrate_approx_hint_fulldim(self, center, covariance): | |||||
| raise NotImplementedError("This method is not generic.") | |||||
| @hint_integration_wrapper() | |||||
| def integrate_short_vector_hint(self, v): | |||||
| raise NotImplementedError("This method is not generic.") | |||||
| def volumes(self): | |||||
| raise NotImplementedError("This method is not generic.") | |||||
| def dim(self): | |||||
| raise NotImplementedError("This method is not generic.") | |||||
| def test_primitive_dual(self, V, action): | |||||
| raise NotImplementedError("This method is not generic.") | |||||
| def estimate_attack(self, probabilistic=False, tours=1, silent=False): | |||||
| """ Assesses the complexity of the lattice attack on the instance. | |||||
| Return value in Bikz | |||||
| """ | |||||
| (Bvol, Svol, dvol) = self.volumes() | |||||
| dim_ = self.dim() | |||||
| beta, delta = compute_beta_delta( | |||||
| dim_, dvol, probabilistic=probabilistic, tours=tours) | |||||
| self.dvol = dvol | |||||
| self.delta = delta | |||||
| self.beta = beta | |||||
| if self.verbosity and not silent: | |||||
| self.logging(" Attack Estimation ", style="HEADER") | |||||
| self.logging("ln(dvol)=%4.7f \t ln(Bvol)=%4.7f \t ln(Svol)=%4.7f \t" | |||||
| % (dvol, Bvol, Svol) + | |||||
| "δ(β)=%.6f" % compute_delta(beta), | |||||
| style="DATA", priority=2) | |||||
| self.logging("dim=%3d \t δ=%.6f \t β=%3.2f " % | |||||
| (dim_, delta, beta), style="VALUE") | |||||
| self.logging("") | |||||
| return (beta, delta) | |||||
| def attack(self, beta_max=None, beta_pre=None, randomize=False, tours=1): | |||||
| raise NotImplementedError( | |||||
| "The generic class is not meant to be used directly.") | |||||
| def S_diag(self): | |||||
| raise NotImplementedError( | |||||
| "The generic class is not meant to be used directly.") | |||||
| def integrate_q_vectors(self, q, min_dim=0, report_every=1, indices=None): | |||||
| self.logging(" Integrating q-vectors ", style="HEADER") | |||||
| Sd = self.S_diag() | |||||
| n = len(Sd) | |||||
| I = [] | |||||
| J = [] | |||||
| M = q * identity_matrix(n - 1) | |||||
| it = 0 | |||||
| verbosity = self.verbosity | |||||
| if indices is None: | |||||
| indices = range(n - 1) | |||||
| while self.dim() > min_dim: | |||||
| if (it % report_every == 0) and report_every > 1: | |||||
| self.logging("[...%d]" % report_every, newline=False) | |||||
| Sd = self.S_diag() | |||||
| L = [(Sd[i], i) for i in indices if i not in I] | |||||
| _, i = max(L) | |||||
| I += [i] | |||||
| try: | |||||
| didit = self.integrate_short_vector_hint( | |||||
| vec(M[i]), catch_invalid_hint=False) | |||||
| if not didit: | |||||
| break | |||||
| J += [i] | |||||
| except InvalidHint as err: | |||||
| self.logging(str(err) + ", Invalid.", | |||||
| style="REJECT", priority=1, newline=True) | |||||
| it += 1 | |||||
| self.verbosity = verbosity if (it % report_every == 0) else 0 | |||||
| self.verbosity = verbosity | |||||
| return [vec(M[i]) for i in J] |
+ 194
- 0
framework/DBDD_predict.sage
Прегледај датотеку
| from fpylll import * | |||||
| from math import log | |||||
| load("../framework/DBDD_generic.sage") | |||||
| load("../framework/proba_utils.sage") | |||||
| class DBDD_predict(DBDD_generic): | |||||
| """ | |||||
| This class defines all the elements defining a DBDD instance | |||||
| in a prediction mode | |||||
| """ | |||||
| def __init__(self, B, S, mu, u=None, verbosity=1, **kwargs): | |||||
| self.Bvol = kwargs.get('Bvol', logdet(B)) | |||||
| self.verbosity = verbosity | |||||
| self.S = S | |||||
| self._dim = S.nrows() | |||||
| self.PP = 0 * S # Span of the projections so far (orthonormal) | |||||
| # Orthogonal span of the intersection so far so far (orthonormal) | |||||
| self.PI = 0 * S | |||||
| self.PI[-1, -1] = 1 | |||||
| self.u = u | |||||
| self.u_original = u | |||||
| self.projections = 0 | |||||
| self.save = {"save": None} | |||||
| self.can_constraints = S.nrows() * [1] | |||||
| self.can_constraints[-1] = None | |||||
| self.estimate_attack(silent=True) | |||||
| def dim(self): | |||||
| return self._dim | |||||
| def S_diag(self): | |||||
| return [self.S[i, i] for i in range(self.S.nrows())] | |||||
| def volumes(self): | |||||
| Bvol = self.Bvol | |||||
| Svol = logdet(self.S + self.PP + self.PI) | |||||
| dvol = Bvol - Svol / 2. | |||||
| return (Bvol, Svol, dvol) | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper(force=True) | |||||
| def integrate_perfect_hint(self, v, l): | |||||
| V = concatenate(v, -l) | |||||
| for i in range(self.S.nrows()): | |||||
| if V[0, i]: | |||||
| self.can_constraints[i] = None | |||||
| V -= V * self.PI | |||||
| den = scal(V * V.T) | |||||
| if den == 0: | |||||
| raise RejectedHint("Redundant hint") | |||||
| self.PI += V.T * (V / den) | |||||
| VS = V * self.S | |||||
| self.Bvol += log(den) / 2 | |||||
| self._dim -= 1 | |||||
| den = scal(VS * V.T) | |||||
| self.S -= VS.T * (VS / den) | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper(force=True) | |||||
| def integrate_modular_hint(self, v, l, k, smooth=True): | |||||
| V = concatenate(v, -l) | |||||
| for i in range(self.S.nrows()): | |||||
| if V[0, i] and self.can_constraints[i] is not None: | |||||
| f = (k / V[0, i]).numerator() | |||||
| self.can_constraints[i] = lcm(f, self.can_constraints[i]) | |||||
| VS = V * self.S | |||||
| den = scal(VS * V.T) | |||||
| if den == 0: | |||||
| raise RejectedHint("Redundant hint") | |||||
| if not smooth: | |||||
| raise NotImplementedError() | |||||
| self.Bvol += log(k) | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper(force=True) | |||||
| def integrate_approx_hint(self, v, l, variance, aposteriori=False): | |||||
| if variance < 0: | |||||
| raise InvalidHint("variance must be non-negative !") | |||||
| if variance == 0: | |||||
| raise InvalidHint("variance=0 : must use perfect hint !") | |||||
| V = concatenate(v, 0) | |||||
| if not aposteriori: | |||||
| VS = V * self.S | |||||
| d = scal(VS * V.T) | |||||
| self.S -= (1 / (variance + d) * VS.T) * VS | |||||
| else: | |||||
| VS = V * self.S | |||||
| # test if eigenvector | |||||
| #if not scal(VS * V.T)**2 == scal(VS * VS.T) * scal(V * V.T): | |||||
| #raise RejectedHint("Not an eigenvector of Σ,") | |||||
| if not scal(VS * VS.T): | |||||
| raise RejectedHint("0-Eigenvector of Σ forbidden,") | |||||
| # New formulae | |||||
| den = scal(VS * V.T) | |||||
| self.S += (((variance - den) / den**2) * VS.T ) * VS | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper() | |||||
| def integrate_approx_hint_fulldim(self, center, | |||||
| covariance, aposteriori=False): | |||||
| # Using http://www.cs.columbia.edu/~liulp/pdf/linear_normal_dist.pdf | |||||
| # with A = Id | |||||
| if not aposteriori: | |||||
| d = self.S.nrows() - 1 | |||||
| if self.S.rank() != d or covariance.rank() != d: | |||||
| raise InvalidHint("Covariances not full dimensional") | |||||
| zero = vec(d * [0]) | |||||
| F = (self.S + block4(covariance, zero.T, zero, vec([1]))).inverse() | |||||
| F[-1, -1] = 0 | |||||
| self.S -= self.S * F * self.S | |||||
| else: | |||||
| raise NotImplementedError() | |||||
| @hint_integration_wrapper(force=False) | |||||
| def integrate_short_vector_hint(self, v): | |||||
| V = concatenate(v, 0) | |||||
| V -= V * self.PP | |||||
| den = scal(V * V.T) | |||||
| if den == 0: | |||||
| raise InvalidHint("Projects to 0,") | |||||
| VPI = V * self.PI | |||||
| if scal(VPI * VPI.T): | |||||
| raise InvalidHint("Not in Span(Λ),") | |||||
| if is_cannonical_direction(v): | |||||
| i, vi = cannonical_param(V) | |||||
| if vi % self.can_constraints[i]: | |||||
| raise InvalidHint("Not in Λ,") | |||||
| else: | |||||
| if self.verbosity: | |||||
| self.logging("Not sure if in Λ,", | |||||
| style="WARNING", newline=False) | |||||
| self.projections += 1 | |||||
| self.Bvol -= log(RR(den)) / 2. | |||||
| self._dim -= 1 | |||||
| self.PP += V.T * (V / den) | |||||
| # This is slower, but equivalent: | |||||
| # PV = identity_matrix(self.S.ncols()) - projection_matrix(V) | |||||
| # X = PV.T * self.S * PV | |||||
| R = (self.S * V.T) * (V / den) | |||||
| self.S -= R | |||||
| L = (V.T / den) * (V * self.S) | |||||
| self.S -= L | |||||
| @not_after_projections | |||||
| @hint_integration_wrapper(force=True) | |||||
| def integrate_q_modular_hint(self, v, l, q): | |||||
| # Copy-Paste of "perfect hint" integration | |||||
| V = concatenate(v, -l) | |||||
| for i in range(self.S.nrows()): | |||||
| if V[0, i]: | |||||
| self.can_constraints[i] = None | |||||
| V -= V * self.PI | |||||
| den = scal(V * V.T) | |||||
| if den == 0: | |||||
| raise RejectedHint("Redundant hint") | |||||
| self.PI += V.T * (V / den) | |||||
| VS = V * self.S | |||||
| self.Bvol += log(den) / 2 | |||||
| self._dim -= 1 | |||||
| den = scal(VS * V.T) | |||||
| self.S -= VS.T * (VS / den) | |||||
| def attack(self): | |||||
| self.logging("Can't run the attack in simulation.", style="WARNING") | |||||
| return None |
+ 172
- 0
framework/DBDD_predict_diag.sage
Прегледај датотеку
| from fpylll import * | |||||
| from math import log | |||||
| from copy import copy | |||||
| load("../framework/proba_utils.sage") | |||||
| load("../framework/utils.sage") | |||||
| load("../framework/geometry.sage") | |||||
| load("../framework/DBDD_generic.sage") | |||||
| def cannonical_direction_only(fn): | |||||
| def decorated(self, *args, **kwargs): | |||||
| if not is_cannonical_direction(args[0]): | |||||
| raise InvalidHint( | |||||
| "Input hint vector must have a cannonical direction") | |||||
| return fn(self, *args, **kwargs) | |||||
| return decorated | |||||
| class DBDD_predict_diag(DBDD_generic): | |||||
| """ | |||||
| This class defines all the elements defining a DBDD instance in a diagonal | |||||
| prediction mode | |||||
| """ | |||||
| def __init__(self, B, S, mu, u=None, verbosity=1, **kwargs): | |||||
| """constructor that builds a DBDD instance from a lattice, mean, sigma | |||||
| and a target | |||||
| ;min_dim: Number of coordinates to find to consider the problem solved | |||||
| :B: Basis of the lattice | |||||
| :S: The Covariance matrix (Sigma) of the uSVP solution | |||||
| :mu: The expectation of the uSVP solution | |||||
| :u: The unique vector to be found (optinal, for verification purposes) | |||||
| :fp_type: Floating point type to use in FPLLL ("d, ld, dd, qd, mpfrX") | |||||
| """ | |||||
| self.verbosity = verbosity | |||||
| if not is_diagonal(S): | |||||
| raise ValueError("given Σ not diagonal") | |||||
| self.S = np.array([RR(S[i, i]) for i in range(S.nrows())]) | |||||
| self.PP = 0 * self.S # Span of the projections so far (orthonormal) | |||||
| # Orthogonal span of the intersection so far so far (orthonormal) | |||||
| self.PI = 0 * self.S | |||||
| self.PI[-1] = 1 | |||||
| self.u = u | |||||
| self.u_original = u | |||||
| self._dim = S.nrows() | |||||
| self.projections = 0 | |||||
| self.Bvol = kwargs.get('Bvol', logdet(B)) | |||||
| self.save = {"save": None} | |||||
| self.can_constraints = S.nrows() * [1] | |||||
| self.can_constraints[-1] = None | |||||
| self.estimate_attack(silent=True) | |||||
| def dim(self): | |||||
| return self._dim | |||||
| def S_diag(self): | |||||
| return copy(self.S) | |||||
| def volumes(self): | |||||
| Bvol = self.Bvol | |||||
| Svol = sum([log(abs(x)) for x in (self.S + self.PP + self.PI)]) | |||||
| dvol = Bvol - Svol / 2. | |||||
| return (Bvol, Svol, dvol) | |||||
| @cannonical_direction_only | |||||
| @hint_integration_wrapper(force=True) | |||||
| def integrate_perfect_hint(self, V, l): | |||||
| i, vi = cannonical_param(V) | |||||
| self.can_constraints[i] = None | |||||
| if self.PI[i]: | |||||
| raise RejectedHint("Redundant hint, Rejected.") | |||||
| if self.PP[i]: | |||||
| raise InvalidHint("This direction has been projected out.") | |||||
| assert(vi) | |||||
| self.PI[i] = 1 | |||||
| self.S[i] = 0 | |||||
| self.Bvol += log(vi) | |||||
| self._dim -= 1 | |||||
| @cannonical_direction_only | |||||
| @hint_integration_wrapper(force=True) | |||||
| def integrate_modular_hint(self, V, l, k, smooth=True): | |||||
| i, vi = cannonical_param(V) | |||||
| f = (k / vi).numerator() | |||||
| self.can_constraints[i] = lcm(f, self.can_constraints[i]) | |||||
| # vs = vi * self.S[i] | |||||
| den = vi**2 * self.S[i] | |||||
| if den == 0: | |||||
| raise RejectedHint("Redundant hint, Rejected.") | |||||
| if self.PP[i]: | |||||
| raise InvalidHint("This direction has been projected out.") | |||||
| if not smooth: | |||||
| raise NotImplementedError() | |||||
| self.Bvol += log(k) | |||||
| @cannonical_direction_only | |||||
| @hint_integration_wrapper(force=True) | |||||
| def integrate_approx_hint(self, V, l, variance, aposteriori=False): | |||||
| if variance < 0: | |||||
| raise InvalidHint("variance must be non-negative !") | |||||
| if variance == 0: | |||||
| raise InvalidHint("variance=0 : must use perfect hint !") | |||||
| i, vi = cannonical_param(V) | |||||
| vs = vi * self.S[i] | |||||
| if self.PP[i]: | |||||
| raise InvalidHint("This direction has been projected out.") | |||||
| if not aposteriori: | |||||
| d = vs * vi | |||||
| self.S[i] -= (1 / (variance + d) * vs) * vs | |||||
| else: | |||||
| if not vs: | |||||
| raise RejectedHint("0-Eigenvector of Σ forbidden,") | |||||
| den = vi**2 | |||||
| self.S[i] = variance / den | |||||
| @hint_integration_wrapper() | |||||
| def integrate_approx_hint_fulldim(self, center, covariance, aposteriori=False): | |||||
| # Using http://www.cs.columbia.edu/~liulp/pdf/linear_normal_dist.pdf | |||||
| # with A = Id | |||||
| if not is_diagonal(covariance): | |||||
| raise ValueError("given covariance not diagonal") | |||||
| if not aposteriori: | |||||
| d = len(self.S) - 1 | |||||
| for i in range(d): | |||||
| if covariance[i, i] == 0: | |||||
| raise InvalidHint("Covariances not full dimensional") | |||||
| for i in range(d): | |||||
| self.S[i] -= self.S[i]**2 / (self.S[i] + covariance[i, i]) | |||||
| # F = (self.S + block4(covariance, zero.T, zero, vec([1]))).inverse() | |||||
| # F[-1,-1] = 0 | |||||
| # self.S -= self.S * F * self.S | |||||
| else: | |||||
| raise NotImplementedError() | |||||
| @cannonical_direction_only | |||||
| @hint_integration_wrapper(force=False) | |||||
| def integrate_short_vector_hint(self, V): | |||||
| i, vi = cannonical_param(V) | |||||
| vi -= vi * self.PP[i] | |||||
| den = vi**2 | |||||
| if den == 0: | |||||
| raise InvalidHint("Redundant hint,") | |||||
| viPI = vi * self.PI[i] | |||||
| if viPI**2: | |||||
| raise InvalidHint("Not in Span(Λ),") | |||||
| if vi % self.can_constraints[i]: | |||||
| raise InvalidHint("Not in Λ,") | |||||
| self.projections += 1 | |||||
| self.Bvol -= log(RR(den)) / 2. | |||||
| self._dim -= 1 | |||||
| self.PP[i] = 1 | |||||
| self.S[i] = 0 | |||||
| def attack(self): | |||||
| self.logging("Can't run the attack in simulation.", style="WARNING") | |||||
| return None |
+ 21
- 0
framework/__init__.py
Прегледај датотеку
| import os | |||||
| # Save the original working directory | |||||
| _cname = os.getcwd() | |||||
| #print('Original: %s' % os.getcwd()) | |||||
| # Define the right working directory for the module | |||||
| abspath = os.path.abspath(__file__) | |||||
| _dname = os.path.dirname(abspath) | |||||
| os.chdir(_dname) | |||||
| #print('New: %s' % os.getcwd()) | |||||
| # Import the module | |||||
| from sage.all_cmdline import * | |||||
| _sage_const_1 = Integer(1); _sage_const_0 = Integer(0); _sage_const_2 = Integer(2); _sage_const_4 = Integer(4); _sage_const_16 = Integer(16); _sage_const_8 = Integer(8); _sage_const_3 = Integer(3) | |||||
| load("instance_gen.sage") | |||||
| # Come back with the original working directory | |||||
| os.chdir(_cname) | |||||
| #print('Come back: %s' % os.getcwd()) | |||||
BIN
framework/__pycache__/__init__.cpython-37.pyc
Прегледај датотеку
BIN
framework/__pycache__/instance_gen.cpython-37.pyc
Прегледај датотеку
BIN
framework/__pycache__/test.cpython-37.pyc
Прегледај датотеку
BIN
framework/__pycache__/test2.cpython-37.pyc
Прегледај датотеку
+ 97680
- 0
framework/bkz_strat.json
Разлика између датотеке није приказан због своје велике величине
Прегледај датотеку
+ 308
- 0
framework/geometry.sage
Прегледај датотеку
| from numpy.linalg import inv as np_inv | |||||
| # from numpy.linalg import slogdet as np_slogdet | |||||
| from numpy import array | |||||
| import numpy as np | |||||
| def dual_basis(B): | |||||
| """ | |||||
| Compute the dual basis of B | |||||
| """ | |||||
| return B.pseudoinverse().transpose() | |||||
| def projection_matrix(A): | |||||
| """ | |||||
| Construct the projection matrix orthogonally to Span(V) | |||||
| """ | |||||
| S = A * A.T | |||||
| return A.T * S.inverse() * A | |||||
| def project_against(v, X): | |||||
| """ Project matrix X orthonally to vector v""" | |||||
| # Pv = projection_matrix(v) | |||||
| # return X - X * Pv | |||||
| Z = (X * v.T) * v / scal(v * v.T) | |||||
| return X - Z | |||||
| # def make_primitive(B, v): | |||||
| # assert False | |||||
| # # project and Scale v's in V so that each v | |||||
| # # is in the lattice, and primitive in it. | |||||
| # # Note: does not make V primitive as as set of vector ! | |||||
| # # (e.g. linear dep. not eliminated) | |||||
| # PB = projection_matrix(B) | |||||
| # DT = dual_basis(B).T | |||||
| # v = vec(v) * PB | |||||
| # w = v * DT | |||||
| # den = lcm([x.denominator() for x in w[0]]) | |||||
| # num = gcd([x for x in w[0] * den]) | |||||
| # if num==0: | |||||
| # return None | |||||
| # v *= den/num | |||||
| # return v | |||||
| def vol(B): | |||||
| return sqrt(det(B * B.T)) | |||||
| def project_and_eliminate_dep(B, W): | |||||
| # Project v on Span(B) | |||||
| PB = projection_matrix(B) | |||||
| V = W * PB | |||||
| rank_loss = V.nrows() - V.rank() | |||||
| if rank_loss > 0: | |||||
| print("WARNING: their were %d linear dependencies out of %d " % | |||||
| (rank_loss, V.nrows())) | |||||
| V = V.LLL() | |||||
| V = V[rank_loss:] | |||||
| return V | |||||
| def is_cannonical_direction(v): | |||||
| v = vec(v) | |||||
| return sum([x != 0 for x in v[0]]) == 1 | |||||
| def cannonical_param(v): | |||||
| v = vec(v) | |||||
| assert is_cannonical_direction(v) | |||||
| i = [x != 0 for x in v[0]].index(True) | |||||
| return i, v[0, i] | |||||
| def remove_linear_dependencies(B, dim=None): | |||||
| nrows = B.nrows() | |||||
| if dim is None or nrows > dim: | |||||
| #print(f'Go... [{dim}]') | |||||
| B = B.LLL() | |||||
| r = min([i for i in range(B.nrows()) if not B[i].is_zero()]) if dim is None else nrows-dim | |||||
| B = B[r:] | |||||
| #print(f'[{nrows}->{B.nrows()}]') | |||||
| return B | |||||
| def lattice_orthogonal_section(D, V): | |||||
| """ | |||||
| Compute the intersection of the lattice L(B) | |||||
| with the hyperplane orthogonal to Span(V). | |||||
| (V can be either a vector or a matrix) | |||||
| INPUT AND OUTPUT DUAL BASIS | |||||
| Algorithm: | |||||
| - project V onto Span(B) | |||||
| - project the dual basis onto orth(V) | |||||
| - eliminate linear dependencies (LLL) | |||||
| - go back to the primal. | |||||
| """ | |||||
| #V = project_and_eliminate_dep(D, V) ## No need because D is full-rank | |||||
| #r = V.nrows() | |||||
| # Project the dual basis orthogonally to v | |||||
| PV = projection_matrix(V) | |||||
| D = D - D * PV | |||||
| #print(f'LLL... ({return_basis})', end='') | |||||
| # Eliminate linear dependencies | |||||
| #if return_basis: | |||||
| # D = remove_linear_dependencies(D) | |||||
| #print(f'{D.nrows()}') | |||||
| #print('Done.') | |||||
| # Go back to the primal | |||||
| return D | |||||
| def lattice_project_against(B, V): | |||||
| """ | |||||
| Compute the projection of the lattice L(B) orthogonally to Span(V). All vectors if V | |||||
| (or at least their projection on Span(B)) must belong to L(B). | |||||
| Algorithm: | |||||
| - project V onto Span(B) | |||||
| - project the basis onto orth(V) | |||||
| - eliminate linear dependencies (LLL) | |||||
| """ | |||||
| # Project v on Span(B) | |||||
| #V = project_and_eliminate_dep(B, V) ## No need because D is full-rank | |||||
| #r = V.nrows() # Useless | |||||
| # Check that V belogs to L(B) | |||||
| D = dual_basis(B) | |||||
| M = D * V.T | |||||
| if not lcm([x.denominator() for x in M.list()]) == 1: | |||||
| raise ValueError("Not in the lattice") | |||||
| # Project the basis orthogonally to v | |||||
| PV = projection_matrix(V) | |||||
| B = B - B * PV | |||||
| # Eliminate linear dependencies | |||||
| #if return_basis: | |||||
| # B = remove_linear_dependencies(B) | |||||
| # Go back to the primal | |||||
| return B | |||||
| def lattice_modular_intersection(D, V, k): | |||||
| """ | |||||
| Compute the intersection of the lattice L(B) with | |||||
| the lattice {x | x*V = 0 mod k} | |||||
| (V can be either a vector or a matrix) | |||||
| Algorithm: | |||||
| - project V onto Span(B) | |||||
| - append the equations in the dual | |||||
| - eliminate linear dependencies (LLL) | |||||
| - go back to the primal. | |||||
| """ | |||||
| # Project v on Span(B) | |||||
| #V = project_and_eliminate_dep(D, V) ## No need because D is full-rank | |||||
| #r = V.nrows() # Useless | |||||
| # append the equation in the dual | |||||
| V /= k | |||||
| # D = dual_basis(B) | |||||
| D = D.stack(V) | |||||
| # Eliminate linear dependencies | |||||
| #if return_basis: | |||||
| # D = remove_linear_dependencies(D) | |||||
| # Go back to the primal | |||||
| return D | |||||
| def is_diagonal(M): | |||||
| if M.nrows() != M.ncols(): | |||||
| return False | |||||
| A = M.numpy() | |||||
| return np.all(A == np.diag(np.diagonal(A))) | |||||
| def logdet(M, exact=False): | |||||
| """ | |||||
| Compute the log of the determinant of a large rational matrix, | |||||
| tryping to avoid overflows. | |||||
| """ | |||||
| if not exact: | |||||
| MM = array(M, dtype=float) | |||||
| _, l = slogdet(MM) | |||||
| return l | |||||
| a = abs(M.det()) | |||||
| l = 0 | |||||
| while a > 2**32: | |||||
| l += RR(32 * ln(2)) | |||||
| a /= 2**32 | |||||
| l += ln(RR(a)) | |||||
| return l | |||||
| def degen_inverse(S, B=None): | |||||
| """ Compute the inverse of a symmetric matrix restricted | |||||
| to its span | |||||
| """ | |||||
| # Get an orthogonal basis for the Span of B | |||||
| if B is None: | |||||
| # Get an orthogonal basis for the Span of B | |||||
| V = S.echelon_form() | |||||
| V = V[:V.rank()] | |||||
| P = projection_matrix(V) | |||||
| else: | |||||
| P = projection_matrix(B) | |||||
| # make S non-degenerated by adding the complement of span(B) | |||||
| C = identity_matrix(S.ncols()) - P | |||||
| Sinv = (S + C).inverse() - C | |||||
| assert S * Sinv == P, "Consistency failed (probably not your fault)." | |||||
| assert P * Sinv == Sinv, "Consistency failed (probably not your fault)." | |||||
| return Sinv | |||||
| def degen_logdet(S, B=None): | |||||
| """ Compute the determinant of a symmetric matrix | |||||
| sigma (m x m) restricted to the span of the full-rank | |||||
| rectangular (k x m, k <= m) matrix V | |||||
| """ | |||||
| # Get an orthogonal basis for the Span of B | |||||
| if B is None: | |||||
| # Get an orthogonal basis for the Span of B | |||||
| V = S.echelon_form() | |||||
| V = V[:V.rank()] | |||||
| P = projection_matrix(V) | |||||
| else: | |||||
| P = projection_matrix(B) | |||||
| # Check that S is indeed supported by span(B) | |||||
| #assert S == P.T * S * P | |||||
| assert (S - P.T * S * P).norm() <= 1e-10 | |||||
| # make S non-degenerated by adding the complement of span(B) | |||||
| C = identity_matrix(S.ncols()) - P | |||||
| l3 = logdet(S + C) | |||||
| return l3 | |||||
| def square_root_inverse_degen(S, B=None): | |||||
| """ Compute the determinant of a symmetric matrix | |||||
| sigma (m x m) restricted to the span of the full-rank | |||||
| rectangular (k x m, k <= m) matrix V | |||||
| """ | |||||
| if B is None: | |||||
| # Get an orthogonal basis for the Span of B | |||||
| V = S.echelon_form() | |||||
| V = V[:V.rank()] | |||||
| P = projection_matrix(V) | |||||
| else: | |||||
| P = projection_matrix(B) | |||||
| # make S non-degenerated by adding the complement of span(B) | |||||
| C = identity_matrix(S.ncols()) - P | |||||
| S_inv = np_inv(array((S + C), dtype=float)) | |||||
| S_inv = array(S_inv, dtype=float) | |||||
| L_inv = cholesky(S_inv) | |||||
| L_inv = round_matrix_to_rational(L_inv) | |||||
| L = L_inv.inverse() | |||||
| return L, L_inv | |||||
| def build_standard_substitution_matrix(V, pivot=None, data=None, output_data=False): | |||||
| _, pivot = V.nonzero_positions()[0] if (pivot is None) else (None, pivot) | |||||
| assert V[0,pivot] != 0, 'The value of the pivot must be non-zero.' | |||||
| dim = V.ncols() | |||||
| V1 = - V[0,:pivot] / V[0,pivot] | |||||
| V2 = - V[0,pivot+1:] / V[0,pivot] | |||||
| Gamma = zero_matrix(QQ, dim,dim-1) | |||||
| Gamma[:pivot,:pivot] = identity_matrix(pivot) | |||||
| Gamma[pivot,:pivot] = V1 | |||||
| Gamma[pivot,pivot:] = V2 | |||||
| Gamma[pivot+1:,pivot:] = identity_matrix(dim-pivot-1) | |||||
| data = data if not output_data else {} | |||||
| if data is not None: | |||||
| norm2 = 1 + scal(V1*V1.T) + scal(V2*V2.T) | |||||
| normalization_matrix = zero_matrix(QQ, dim-1,dim-1) | |||||
| normalization_matrix[:pivot,:pivot] = identity_matrix(pivot) - V1.T*V1 / norm2 | |||||
| normalization_matrix[pivot:,pivot:] = identity_matrix(dim-pivot-1) - V2.T*V2 / norm2 | |||||
| normalization_matrix[:pivot,pivot:] = - V1.T*V2 / norm2 | |||||
| normalization_matrix[pivot:,:pivot] = - V2.T*V1 / norm2 | |||||
| data['det'] = norm2 | |||||
| data['normalization_matrix'] = normalization_matrix | |||||
| if output_data: | |||||
| return Gamma, data | |||||
| else: | |||||
| return Gamma |
+ 171
- 0
framework/instance_gen.sage
Прегледај датотеку
| from random import shuffle, randint | |||||
| load("../framework/proba_utils.sage") | |||||
| load("../framework/DBDD_predict_diag.sage") | |||||
| load("../framework/DBDD_predict.sage") | |||||
| load("../framework/DBDD.sage") | |||||
| def initialize_from_LWE_instance(dbdd_class, n, q, m, D_e, | |||||
| D_s, diag=False, verbosity=1): | |||||
| """ | |||||
| constructor that builds a DBDD instance from a LWE instance | |||||
| :n: (integer) size of the secret s | |||||
| :q: (integer) modulus | |||||
| :m: (integer) size of the error e | |||||
| :D_e: distribution of the error e (dictionnary form) | |||||
| :D_s: distribution of the secret s (dictionnary form) | |||||
| """ | |||||
| if verbosity: | |||||
| logging(" Build DBDD from LWE ", style="HEADER") | |||||
| logging("n=%3d \t m=%3d \t q=%d" % (n, m, q), style="VALUE") | |||||
| # define the mean and sigma of the instance | |||||
| mu_e, s_e = average_variance(D_e) | |||||
| mu_s, s_s = average_variance(D_s) | |||||
| mu = vec(m * [mu_e] + n * [mu_s] + [1]) | |||||
| S = diagonal_matrix(m * [s_e] + n * [s_s] + [0]) | |||||
| # draw matrix A and define the lattice | |||||
| A = matrix([[randint(0, q) for _ in range(n)] for _ in range(m)]) | |||||
| B = build_LWE_lattice(-A, q) | |||||
| D = build_LWE_lattice(A/q, 1/q) | |||||
| # draw the secrets | |||||
| s = vec([draw_from_distribution(D_s) for _ in range(n)]) | |||||
| e = vec([draw_from_distribution(D_e) for _ in range(m)]) | |||||
| # compute the public value t and build a target | |||||
| b = (s * A.T + e) % q | |||||
| tar = concatenate([b, [0] * n]) | |||||
| B = kannan_embedding(B, tar) | |||||
| D = kannan_embedding(D, concatenate([-b/q, [0] * n])).T | |||||
| u = concatenate([e, s, [1]]) | |||||
| return A, b, dbdd_class(B, S, mu, u, verbosity=verbosity, D=D, Bvol=m*log(q)) | |||||
| def initialize_from_LWR_instance(dbdd_class, n, q, p, m, D_s, verbosity=1): | |||||
| if verbosity: | |||||
| logging(" Build DBDD from LWR ", style="HEADER") | |||||
| logging("n=%3d \t m=%3d \t q=%d \t p=%d" % (n, m, q, p), style="VALUE") | |||||
| D_e = build_mod_switching_error_law(q, p) | |||||
| # draw matrix A and define the lattice | |||||
| A = matrix([[randint(0, q) for _ in range(n)] for _ in range(m)]) | |||||
| s = vec([draw_from_distribution(D_s) for _ in range(n)]) | |||||
| B = build_LWE_lattice(-A, q) | |||||
| b = q / p * ((p / q) * s * A.T).apply_map(lambda x: x.round(mode='down')) | |||||
| e = b - s * A.T | |||||
| tar = concatenate([b, [0] * n]) | |||||
| B = kannan_embedding(B, tar) | |||||
| u = concatenate([e, s, [1]]) | |||||
| # define the mean and sigma of the instance | |||||
| mu_e, s_e = average_variance(D_e) | |||||
| mu_s, s_s = average_variance(D_s) | |||||
| mu = vec(m * [mu_e] + n * [mu_s] + [1]) | |||||
| S = diagonal_matrix(m * [s_e] + n * [s_s] + [0]) | |||||
| return A, b, dbdd_class(B, S, mu, u, verbosity=verbosity) | |||||
| def initialize_round5_instance(dbdd_class, n, q, p, h, m, D_e, | |||||
| D_s, verbosity=1): | |||||
| if verbosity: | |||||
| logging(" Build DBDD from round5 ", style="HEADER") | |||||
| logging("n=%3d \t m=%3d \t q=%d \t p=%d" % (n, m, q, p), style="VALUE") | |||||
| # draw matrix A and define the lattice | |||||
| assert (h % 2 == 0), "Round5 requires 2 to divide h" | |||||
| A = matrix([[randint(0, q) for _ in range(n)] for _ in range(m)]) | |||||
| s = h / 2 * [1] + h / 2 * [-1] + (n - h) * [0] | |||||
| shuffle(s) | |||||
| s = vec(s) | |||||
| B = build_LWE_lattice(-A, q) | |||||
| b = vec([q / p * (round((p / q) * ((s * A.T)[0][i] % q)) % p) | |||||
| for i in range(n)]) | |||||
| e = vec([((- s * A.T)[0][i] + b[0][i]) % q | |||||
| if ((- s * A.T)[0][i] + b[0][i]) % q < q / 2 | |||||
| else ((- s * A.T)[0][i] + b[0][i]) % q - q | |||||
| for i in range(n)]) | |||||
| tar = concatenate([b, [0] * n]) | |||||
| B = kannan_embedding(B, tar) | |||||
| u = concatenate([e, s, [1]]) | |||||
| # define the mean and sigma of the instance | |||||
| mu_e, s_e = average_variance(D_e) | |||||
| mu_s, s_s = average_variance(D_s) | |||||
| mu = vec(m * [mu_e] + n * [mu_s] + [1]) | |||||
| S = diagonal_matrix(m * [s_e] + n * [s_s] + [0]) | |||||
| return A, b, dbdd_class(B, S, mu, u, verbosity=verbosity) | |||||
| def initialize_LAC_instance(dbdd_class, n, q, m, D_e, D_s, verbosity=1): | |||||
| if verbosity: | |||||
| logging(" Build DBDD for LAC ", style="HEADER") | |||||
| logging("n=%3d \t m=%3d \t q=%d" % (n, m, q), style="VALUE") | |||||
| # draw matrix A and define the lattice | |||||
| A = matrix([[randint(0, q) for _ in range(n)] for _ in range(m)]) | |||||
| B = build_LWE_lattice(-A, q) | |||||
| assert (n % 4 == 0) and (m % 4 == 0), "LAC requires 4 to divide n and m" | |||||
| s = (n / 4) * [0, 1, 0, -1] | |||||
| shuffle(s) | |||||
| s = vec(s) | |||||
| e = (m / 4) * [0, 1, 0, -1] | |||||
| shuffle(e) | |||||
| e = vec(e) | |||||
| b = (s * A.T + e) % q | |||||
| tar = concatenate([b, [0] * n]) | |||||
| B = kannan_embedding(B, tar) | |||||
| u = concatenate([e, s, [1]]) | |||||
| # define the mean and sigma of the instance | |||||
| mu_e, s_e = average_variance(D_e) | |||||
| mu_s, s_s = average_variance(D_s) | |||||
| mu = vec(m * [mu_e] + n * [mu_s] + [1]) | |||||
| S = diagonal_matrix(m * [s_e] + n * [s_s] + [0]) | |||||
| return A, b, dbdd_class(B, S, mu, u, verbosity=verbosity) | |||||
| def initialize_NTRU_instance(dbdd_class, n, q, m, D_e, D_s, verbosity=1): | |||||
| if verbosity: | |||||
| logging(" Build DBDD for NTRU HPS VERSION ", style="HEADER") | |||||
| logging("n=%3d \t m=%3d \t q=%d" % (n, m, q), style="VALUE") | |||||
| assert (q % 16 == 0), "NTRU-HPS requires 16 to divide q" | |||||
| A = matrix([[randint(0, q) for _ in range(n)] for _ in range(m)]) | |||||
| B = build_LWE_lattice(-A, q) | |||||
| if q / 8 - 2 <= 2 * n / 3: | |||||
| hamming_weight = (q / 16 - 1) | |||||
| else: | |||||
| hamming_weight = floor(n / 3) | |||||
| s = hamming_weight * [1] + hamming_weight * \ | |||||
| [-1] + (n - 2 * hamming_weight) * [0] | |||||
| shuffle(s) | |||||
| s = vec(s) | |||||
| e = vec([draw_from_distribution(D_e) for _ in range(m)]) | |||||
| b = (s * A.T + e) % q | |||||
| tar = concatenate([b, [0] * n]) | |||||
| B = kannan_embedding(B, tar) | |||||
| u = concatenate([e, s, [1]]) | |||||
| # define the mean and sigma of the instance | |||||
| mu_e, s_e = average_variance(D_e) | |||||
| mu_s, s_s = average_variance(D_s) | |||||
| mu = vec(m * [mu_e] + n * [mu_s] + [1]) | |||||
| S = diagonal_matrix(m * [s_e] + n * [s_s] + [0]) | |||||
| return A, b, dbdd_class(B, S, mu, u, verbosity=verbosity) | |||||
| # def initialize_NTRU_prime_instance(dbdd_class, n, q, m, h, D_f, | |||||
| # D_g, verbosity=1): | |||||
| # if verbosity: | |||||
| # logging(" Build DBDD for NTRU PRIME VERSION ", style="HEADER") | |||||
| # logging("n=%3d \t m=%3d \t q=%d \t h=%d" % (n, m, q, h), style="VALUE") | |||||
| # A = matrix([[randint(0, q) for _ in range(n)] for _ in range(m)]) | |||||
| # B = build_LWE_lattice(-A, q) | |||||
| # e = h * [1] + (n - h) * [0] | |||||
| # shuffle(e) | |||||
| # e = [(-1) ** randint(0, 1) * e[i] for i in range(len(e))] | |||||
| # e = vec(e) | |||||
| # s = vec([draw_from_distribution(D_g) for _ in range(m)]) | |||||
| # b = (s * A.T + e) % q | |||||
| # tar = concatenate([b, [0] * n]) | |||||
| # B = kannan_embedding(B, tar) | |||||
| # u = concatenate([e, s, [1]]) | |||||
| # # define the mean and sigma of the instance | |||||
| # mu_e, s_e = average_variance(D_g) | |||||
| # mu_s, s_s = average_variance(D_f) | |||||
| # mu = vec(m * [mu_e] + n * [mu_s] + [1]) | |||||
| # S = diagonal_matrix(m * [s_e] + n * [s_s] + [0]) | |||||
| # return A, b, dbdd_class(B, S, mu, u, verbosity=verbosity) |
+ 17
- 0
framework/load_strategies.sage
Прегледај датотеку
| # Apparently the internal loader for | |||||
| # strategies of fplll/fpylll is broken through sage | |||||
| # Doing that by hand... | |||||
| import json | |||||
| from fpylll.fplll.bkz_param import Strategy | |||||
| with open("../framework/bkz_strat.json") as json_data: | |||||
| data = json.load(json_data) | |||||
| strategies = 91 * [None] | |||||
| for datum in data: | |||||
| b = datum["block_size"] | |||||
| prun = datum["pruning_parameters"] | |||||
| prep = datum["preprocessing_block_sizes"] | |||||
| strat = Strategy(b, prep, prun) | |||||
| strategies[b] = strat |
+ 188
- 0
framework/proba_utils.sage
Прегледај датотеку
| from math import factorial as fac | |||||
| from math import ceil, erf, sqrt, exp | |||||
| def build_Gaussian_law(sigma, t): | |||||
| D = {} | |||||
| for i in range(0, t + 1): | |||||
| D[i] = exp(-i ** 2 / (2 * sigma ** 2)) | |||||
| D[-i] = D[i] | |||||
| normalization = sum([D[i] for i in D]) | |||||
| for i in D: | |||||
| D[i] = D[i] / normalization | |||||
| assert abs(sum([D[i] for i in range(-t, t + 1)]) - 1.) <= 10 ** -10 | |||||
| return D | |||||
| def gaussian_center_weight(sigma, t): | |||||
| """ Weight of the gaussian of std deviation s, on the interval [-t, t] | |||||
| :param x: (float) | |||||
| :param y: (float) | |||||
| :returns: erf( t / (sigma*sqrt 2) ) | |||||
| """ | |||||
| return erf(t / (sigma * sqrt(2.))) | |||||
| def binomial(x, y): | |||||
| """ Binomial coefficient | |||||
| :param x: (integer) | |||||
| :param y: (integer) | |||||
| :returns: y choose x | |||||
| """ | |||||
| try: | |||||
| binom = fac(x) // fac(y) // fac(x - y) | |||||
| except ValueError: | |||||
| binom = 0 | |||||
| return binom | |||||
| def centered_binomial_pdf(k, x): | |||||
| """ Probability density function of the centered binomial law of param k at x | |||||
| :param k: (integer) | |||||
| :param x: (integer) | |||||
| :returns: p_k(x) | |||||
| """ | |||||
| return binomial(2 * k, x + k) / 2.**(2 * k) | |||||
| def build_centered_binomial_law(k): | |||||
| """ Construct the binomial law as a dictionnary | |||||
| :param k: (integer) | |||||
| :param x: (integer) | |||||
| :returns: A dictionnary {x:p_k(x) for x in {-k..k}} | |||||
| """ | |||||
| D = {} | |||||
| for i in range(-k, k + 1): | |||||
| D[i] = centered_binomial_pdf(k, i) | |||||
| return D | |||||
| def build_uniform_law(p): | |||||
| """ Construct the binomial law as a dictionnary | |||||
| :param k: (integer) | |||||
| :param x: (integer) | |||||
| :returns: A dictionnary {x:p_k(x) for x in {-k..k}} | |||||
| """ | |||||
| D = {} | |||||
| for i in range(p): | |||||
| D[i - p / 2] = 1. / p | |||||
| return D | |||||
| def mod_switch(x, q, rq): | |||||
| """ Modulus switching (rounding to a different discretization of the Torus) | |||||
| :param x: value to round (integer) | |||||
| :param q: input modulus (integer) | |||||
| :param rq: output modulus (integer) | |||||
| """ | |||||
| return int(round(1. * rq * x / q) % rq) | |||||
| def mod_centered(x, q): | |||||
| """ reduction mod q, centered (ie represented in -q/2 .. q/2) | |||||
| :param x: value to round (integer) | |||||
| :param q: input modulus (integer) | |||||
| """ | |||||
| a = x % q | |||||
| if a < q / 2: | |||||
| return a | |||||
| return a - q | |||||
| def build_mod_switching_error_law(q, rq): | |||||
| """ Construct Error law: law of the difference | |||||
| introduced by switching from and back a uniform value mod q | |||||
| :param q: original modulus (integer) | |||||
| :param rq: intermediate modulus (integer) | |||||
| """ | |||||
| D = {} | |||||
| V = {} | |||||
| for x in range(q): | |||||
| y = mod_switch(x, q, rq) | |||||
| z = mod_switch(y, rq, q) | |||||
| d = mod_centered(x - z, q) | |||||
| D[d] = D.get(d, 0) + 1. / q | |||||
| V[y] = V.get(y, 0) + 1 | |||||
| return D | |||||
| def law_convolution(A, B): | |||||
| """ Construct the convolution of two laws | |||||
| (sum of independent variables from two input laws) | |||||
| :param A: first input law (dictionnary) | |||||
| :param B: second input law (dictionnary) | |||||
| """ | |||||
| C = {} | |||||
| for a in A: | |||||
| for b in B: | |||||
| c = a + b | |||||
| C[c] = C.get(c, 0) + A[a] * B[b] | |||||
| return C | |||||
| def law_product(A, B): | |||||
| """ Construct the law of the product of independent | |||||
| variables from two input laws | |||||
| :param A: first input law (dictionnary) | |||||
| :param B: second input law (dictionnary) | |||||
| """ | |||||
| C = {} | |||||
| for a in A: | |||||
| for b in B: | |||||
| c = a * b | |||||
| C[c] = C.get(c, 0) + A[a] * B[b] | |||||
| return C | |||||
| def clean_dist(A): | |||||
| """ Clean a distribution to accelerate furthe | |||||
| computation (drop element of the support | |||||
| with proba less than 2^-300) | |||||
| :param A: input law (dictionnary) | |||||
| """ | |||||
| B = {} | |||||
| for (x, y) in A.items(): | |||||
| if y > 2**(-300): | |||||
| B[x] = y | |||||
| return B | |||||
| def renormalize_dist(A): | |||||
| B = {} | |||||
| summ = sum([y for (x,y) in A.items()]) | |||||
| for x in A: | |||||
| B[x] = A[x] / summ | |||||
| return B | |||||
| def iter_law_convolution(A, i): | |||||
| """ compute the -ith forld convolution of a distribution (using double-and-add) | |||||
| :param A: first input law (dictionnary) | |||||
| :param i: (integer) | |||||
| """ | |||||
| D = {0: 1.0} | |||||
| i_bin = bin(i)[2:] # binary representation of n | |||||
| for ch in i_bin: | |||||
| D = law_convolution(D, D) | |||||
| D = clean_dist(D) | |||||
| if ch == '1': | |||||
| D = law_convolution(D, A) | |||||
| D = clean_dist(D) | |||||
| return D | |||||
| def tail_probability(D, t): | |||||
| ''' | |||||
| Probability that an drawn from D is strictly greater than t in absolute value | |||||
| :param D: Law (Dictionnary) | |||||
| :param t: tail parameter (integer) | |||||
| ''' | |||||
| s = 0 | |||||
| ma = max(D.keys()) | |||||
| if t >= ma: | |||||
| return 0 | |||||
| # Summing in reverse for better numerical precision (assuming tails are decreasing) | |||||
| for i in reversed(range(int(ceil(t)), ma)): | |||||
| s += D.get(i, 0) + D.get(-i, 0) | |||||
| return s |
+ 406
- 0
framework/utils.sage
Прегледај датотеку
| from numpy.random import choice as np_random_choice | |||||
| from numpy.linalg import slogdet, qr, cholesky | |||||
| from numpy import array | |||||
| from math import pi, exp | |||||
| print_style = {'SUCCESS': '\x1b[1;37;42m', | |||||
| 'FAILURE': '\x1b[1;37;41m', | |||||
| 'REJECT': '\x1b[3;31m', | |||||
| 'ACCEPT': '\x1b[3;32m', | |||||
| 'VALUE': '\x1b[1;33m', | |||||
| 'DATA': '\x1b[3;34m', | |||||
| 'WARNING': '\x1b[6;30;43m', | |||||
| 'ACTION': '\x1b[1;37m', | |||||
| 'HEADER': '\x1b[4;37m', | |||||
| 'NORMAL': '\x1b[0m', | |||||
| } | |||||
| def logging(message, style='NORMAL', newline=True): | |||||
| if style is not None: | |||||
| print(print_style[style], end=' ') | |||||
| print(message, end=' ') | |||||
| if newline: | |||||
| print('\x1b[0m') | |||||
| else: | |||||
| print('\x1b[0m', end=' ') | |||||
| sys.stdout.flush() | |||||
| def hint_to_string(v, l=None, lit="u", max_coeffs=5): | |||||
| s = "" | |||||
| count = 0 | |||||
| for i in range(v.ncols()): | |||||
| x = v[0][i] | |||||
| if x == 0: | |||||
| continue | |||||
| count += 1 | |||||
| if count > max_coeffs: | |||||
| s += "+ ... " | |||||
| break | |||||
| if x == 1: | |||||
| if count == 1: | |||||
| s += "%s%d " % (lit, i) | |||||
| else: | |||||
| s += "+ %s%d " % (lit, i) | |||||
| elif x == -1: | |||||
| s += "- %s%d " % (lit, i) | |||||
| elif x > 0 and count == 1: | |||||
| s += "%s*%s%d " % (str(x), lit, i) | |||||
| elif x > 0: | |||||
| s += "+ %s*%s%d " % (str(x), lit, i) | |||||
| else: | |||||
| s += "- %s*%s%d " % (str(-x), lit, i) | |||||
| if l is not None: | |||||
| s += "= %s" % str(l) | |||||
| return s | |||||
| ROUNDING_FACTOR = 2**64 | |||||
| # Vectors will consistently be represented as 1*n matrices | |||||
| def vec(x): | |||||
| # Is this a 2-dim object, with only one row | |||||
| try: | |||||
| x[0][0] | |||||
| try: | |||||
| x[1] | |||||
| except: | |||||
| return matrix(x) | |||||
| raise ValueError( | |||||
| " The object has more than one line: can't convert to vec.") | |||||
| except: | |||||
| # Then it should be a 1 dim object | |||||
| return matrix([x]) | |||||
| def mat(x): | |||||
| return matrix(x) | |||||
| # Convert a 1*1 matrix into a scalar | |||||
| def scal(M): | |||||
| assert M.nrows() == 1 and M.ncols() == 1, "This doesn't seem to be a scalar." | |||||
| return M[0, 0] | |||||
| def average_variance(D): | |||||
| mu = 0. | |||||
| s = 0. | |||||
| for (v, p) in D.items(): | |||||
| mu += v * p | |||||
| s += v * v * p | |||||
| s -= mu * mu | |||||
| return round_to_rational(mu), round_to_rational(s) | |||||
| def canonical_vec(dimension, index): | |||||
| """Returns the vector [0,0 ... 0] with | |||||
| a 1 in a specific index | |||||
| :dimension: integer | |||||
| :index: integer | |||||
| """ | |||||
| v = [0 for _ in range(dimension)] | |||||
| v[index] = 1 | |||||
| return vec(v) | |||||
| def is_canonical_direction(v): | |||||
| """ Test wether the vector has a cannonical direction, and returns | |||||
| its index and length if so, else None, None. | |||||
| """ | |||||
| nz = [x != 0 for x in v] | |||||
| if sum(nz) != 1: | |||||
| return None | |||||
| i = nz.index(True) | |||||
| return i | |||||
| def round_matrix_to_rational(M): | |||||
| A = matrix(ZZ, (ROUNDING_FACTOR * matrix(M)).apply_map(round)) | |||||
| return matrix(QQ, A / ROUNDING_FACTOR) | |||||
| def round_vector_to_rational(v): | |||||
| A = vec(ZZ, (ROUNDING_FACTOR * vec(v)).apply_map(round)) | |||||
| return vec(QQ, A / ROUNDING_FACTOR) | |||||
| def round_to_rational(x): | |||||
| A = ZZ(round(x * ROUNDING_FACTOR)) | |||||
| return QQ(A) / QQ(ROUNDING_FACTOR) | |||||
| def concatenate(L1, L2=None): | |||||
| """ | |||||
| concatenate vecs | |||||
| """ | |||||
| if L2 is None: | |||||
| return vec(sum([list(vec(x)[0]) for x in L1], [])) | |||||
| return vec(list(vec(L1)[0]) + list(vec(L2)[0])) | |||||
| def draw_from_distribution(D): | |||||
| """draw an element from the distribution D | |||||
| :D: distribution in a dictionnary form | |||||
| """ | |||||
| X = np_random_choice([key for key in D.keys()], | |||||
| 1, replace=True, | |||||
| p=[float(prob) for prob in D.values()]) | |||||
| return X[0] | |||||
| def GH_sv_factor_squared(k): | |||||
| return ((pi * k)**(1. / k) * k / (2. * pi * e)) | |||||
| def compute_delta(k): | |||||
| """Computes delta from the block size k. Interpolation from the following | |||||
| data table: | |||||
| Source : https://bitbucket.org/malb/lwe-estimator/ | |||||
| src/9302d4204b4f4f8ceec521231c4ca62027596337/estima | |||||
| tor.py?at=master&fileviewer=file-view-default | |||||
| :k: integer | |||||
| estimator.py table: | |||||
| """ | |||||
| small = {0: 1e20, 1: 1e20, 2: 1.021900, 3: 1.020807, 4: 1.019713, 5: 1.018620, | |||||
| 6: 1.018128, 7: 1.017636, 8: 1.017144, 9: 1.016652, 10: 1.016160, | |||||
| 11: 1.015898, 12: 1.015636, 13: 1.015374, 14: 1.015112, 15: 1.014850, | |||||
| 16: 1.014720, 17: 1.014590, 18: 1.014460, 19: 1.014330, 20: 1.014200, | |||||
| 21: 1.014044, 22: 1.013888, 23: 1.013732, 24: 1.013576, 25: 1.013420, | |||||
| 26: 1.013383, 27: 1.013347, 28: 1.013310, 29: 1.013253, 30: 1.013197, | |||||
| 31: 1.013140, 32: 1.013084, 33: 1.013027, 34: 1.012970, 35: 1.012914, | |||||
| 36: 1.012857, 37: 1.012801, 38: 1.012744, 39: 1.012687, 40: 1.012631, | |||||
| 41: 1.012574, 42: 1.012518, 43: 1.012461, 44: 1.012404, 45: 1.012348, | |||||
| 46: 1.012291, 47: 1.012235, 48: 1.012178, 49: 1.012121, 50: 1.012065} | |||||
| if k != round(k): | |||||
| x = k - floor(k) | |||||
| d1 = compute_delta(floor(x)) | |||||
| d2 = compute_delta(floor(x) + 1) | |||||
| return x * d2 + (1 - x) * d1 | |||||
| k = int(k) | |||||
| if k < 50: | |||||
| return small[k] | |||||
| else: | |||||
| delta = GH_sv_factor_squared(k)**(1. / (2. * k - 2.)) | |||||
| return delta.n() | |||||
| def bkzgsa_gso_len(logvol, i, d, beta=None, delta=None): | |||||
| if delta is None: | |||||
| delta = compute_delta(beta) | |||||
| return RR(delta**(d - 1 - 2 * i) * exp(logvol / d)) | |||||
| rk = [0.789527997160000, 0.780003183804613, 0.750872218594458, 0.706520454592593, 0.696345241018901, 0.660533841808400, 0.626274718790505, 0.581480717333169, 0.553171463433503, 0.520811087419712, 0.487994338534253, 0.459541470573431, 0.414638319529319, 0.392811729940846, 0.339090376264829, 0.306561491936042, 0.276041187709516, 0.236698863270441, 0.196186341673080, 0.161214212092249, 0.110895134828114, 0.0678261623920553, 0.0272807162335610, - | |||||
| 0.0234609979600137, -0.0320527224746912, -0.0940331032784437, -0.129109087817554, -0.176965384290173, -0.209405754915959, -0.265867993276493, -0.299031324494802, -0.349338597048432, -0.380428160303508, -0.427399405474537, -0.474944677694975, -0.530140672818150, -0.561625221138784, -0.612008793872032, -0.669011014635905, -0.713766731570930, -0.754041787011810, -0.808609696192079, -0.859933249032210, -0.884479963601658, -0.886666930030433] | |||||
| simBKZ_c = [None] + [rk[-i] - sum(rk[-i:]) / i for i in range(1, 46)] | |||||
| pruning_proba = .5 | |||||
| simBKZ_c += [RR(log(GH_sv_factor_squared(d)) / 2. - | |||||
| log(pruning_proba) / d) / log(2.) for d in range(46, 1000)] | |||||
| def simBKZ(l, beta, tours=1, c=simBKZ_c): | |||||
| n = len(l) | |||||
| l2 = copy(vector(RR, l)) | |||||
| for k in range(n - 1): | |||||
| d = min(beta, n - k) | |||||
| f = k + d | |||||
| logV = sum(l2[k:f]) | |||||
| lma = logV / d + c[d] | |||||
| if lma >= l2[k]: | |||||
| continue | |||||
| diff = l2[k] - lma | |||||
| l2[k] -= diff | |||||
| for a in range(k + 1, f): | |||||
| l2[a] += diff / (f - k - 1) | |||||
| return l2 | |||||
| chisquared_table = {i: None for i in range(1000)} | |||||
| for i in range(1000): | |||||
| chisquared_table[i] = RealDistribution('chisquared', i) | |||||
| def conditional_chi_squared(d1, d2, lt, l2): | |||||
| """ | |||||
| Probability that a gaussian sample (var=1) of dim d1+d2 has length at most | |||||
| lt knowing that the d2 first cordinates have length at most l2 | |||||
| """ | |||||
| D1 = chisquared_table[d1].cum_distribution_function | |||||
| D2 = chisquared_table[d2].cum_distribution_function | |||||
| l2 = RR(l2) | |||||
| PE2 = D2(l2) | |||||
| steps = 5 * (d1 + d2) | |||||
| # Numerical computation of the integral | |||||
| proba = 0. | |||||
| for i in range(steps)[::-1]: | |||||
| l2_min = i * l2 / steps | |||||
| l2_mid = (i + .5) * l2 / steps | |||||
| l2_max = (i + 1) * l2 / steps | |||||
| PC2 = (D2(l2_max) - D2(l2_min)) / PE2 | |||||
| PE1 = D1(lt - l2_mid) | |||||
| proba += PC2 * PE1 | |||||
| return proba | |||||
| def compute_beta_delta(d, logvol, tours=1, interpolate=True, probabilistic=False): | |||||
| """ | |||||
| Computes the beta value for given dimension and volumes | |||||
| It is assumed that the instance has been normalized and sphericized, | |||||
| i.e. that the covariance matrices of the secret is the identity | |||||
| :d: integer | |||||
| :vol: float | |||||
| """ | |||||
| bbeta = None | |||||
| pprev_margin = None | |||||
| # Keep increasing beta to be sure to catch the second intersection | |||||
| if not probabilistic: | |||||
| for beta in range(2, d): | |||||
| lhs = RR(sqrt(beta)) | |||||
| rhs = bkzgsa_gso_len(logvol, d - beta, d, beta=beta) | |||||
| if lhs < rhs and bbeta is None: | |||||
| margin = rhs / lhs | |||||
| prev_margin = pprev_margin | |||||
| bbeta = beta | |||||
| if lhs > rhs: | |||||
| bbeta = None | |||||
| pprev_margin = rhs / lhs | |||||
| if bbeta is None: | |||||
| return 9999, 0 | |||||
| ddelta = compute_delta(bbeta) * margin**(1. / d) | |||||
| if prev_margin is not None and interpolate: | |||||
| beta_low = log(margin) / (log(margin) - log(prev_margin)) | |||||
| else: | |||||
| beta_low = 0 | |||||
| assert beta_low >= 0 | |||||
| assert beta_low <= 1 | |||||
| return bbeta - beta_low, ddelta | |||||
| else: | |||||
| remaining_proba = 1. | |||||
| average_beta = 0. | |||||
| delta = compute_delta(2) | |||||
| l = [log(bkzgsa_gso_len(logvol, i, d, delta=delta)) / log(2) | |||||
| for i in range(d)] | |||||
| for beta in range(2, d): | |||||
| for t in range(tours): | |||||
| l = simBKZ(l, beta, 1) | |||||
| proba = 1. | |||||
| delta = compute_delta(beta) | |||||
| i = d - beta | |||||
| proba *= chisquared_table[beta].cum_distribution_function( | |||||
| 2**(2 * l[i])) | |||||
| for j in range(2, int(d / beta + 1)): | |||||
| i = d - j * (beta - 1) - 1 | |||||
| xt = 2**(2 * l[i]) | |||||
| if j > 1: | |||||
| x2 = 2**(2 * l[i + (beta - 1)]) | |||||
| d2 = d - i + (beta - 1) | |||||
| proba *= conditional_chi_squared(beta - 1, d2, xt, x2) | |||||
| average_beta += beta * remaining_proba * proba | |||||
| remaining_proba *= 1. - proba | |||||
| if remaining_proba < .001: | |||||
| average_beta += beta * remaining_proba | |||||
| break | |||||
| if remaining_proba > .01: | |||||
| raise ValueError("This instance may be unsolvable") | |||||
| ddelta = compute_delta(average_beta) | |||||
| return average_beta, ddelta | |||||
| def block4(A, B, C, D): | |||||
| return block_matrix([[A, B], [C, D]]) | |||||
| def build_LWE_lattice(A, q): | |||||
| """Builds a n*m matrix of the form | |||||
| q*I, 0 | |||||
| A^T, -I | |||||
| It corresponds to the LWE matrix | |||||
| :A: a m*n matrix | |||||
| :q: integer | |||||
| """ | |||||
| (m, n) = A.nrows(), A.ncols() | |||||
| lambd = block4(q * identity_matrix(m), | |||||
| zero_matrix(ZZ, m, n), | |||||
| A.T, | |||||
| identity_matrix(n) | |||||
| ) | |||||
| return lambd | |||||
| def kannan_embedding(A, target, factor=1): | |||||
| """Creates a kannan embedding, i.e. it appends a line and | |||||
| a column as follows. | |||||
| A, 0 | |||||
| target, uSVP_embedding_coeff | |||||
| :A: a matrix | |||||
| :target: a vector | |||||
| """ | |||||
| d = A.nrows() | |||||
| lambd = block4(A, | |||||
| zero_matrix(ZZ, d, 1), | |||||
| mat(target), | |||||
| mat([factor]) | |||||
| ) | |||||
| return lambd | |||||
| def recenter(elt, q): | |||||
| if elt > q / 2: | |||||
| return elt - q | |||||
| return elt | |||||
| def get_distribution_from_table(table, multiplicative_factor): | |||||
| eta = len(table) | |||||
| D_s = {} | |||||
| support = set() | |||||
| for i in range(eta): | |||||
| D_s[i] = table[i] / multiplicative_factor | |||||
| D_s[-i] = D_s[i] | |||||
| support.add(i) | |||||
| support.add(-i) | |||||
| _, var = average_variance(D_s) | |||||
| assert(abs(sum([D_s[i] for i in support]) - 1) < 1e-5) | |||||
| return D_s |
Loading…
